A Casinha da Matemática Blog
Isto é Matemática – Temporadas
Para acabar de vez com o mito
O “Isto é Matemática” pretende de uma forma simples e realista apresentar a forma como a Matemática nos rodeia em grande parte da nossa vida.
Promovido pela Sociedade Portuguesa de Matemática, apresentado por Rogério Martins, Matemático e Professor Universitário, Direção Criativa de Tiago DaCunha Caetano e com Produção e Realização de Sigma 3, o programa “Isto é Matemática” é emitido pelo canal cabo SIC Notícias.
O Programa teve a sua estreia no dia 13 … Ler mais
Duas variáveis $p$ e $q$
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 38 Ex. 2
Na tabela seguinte, encontra valores correspondentes das variáveis $p$ e $q$.
| $p$ | $1$ | $2$ | $3$ | $4$ |
| $q$ | $950$ | $900$ | $850$ | $800$ |
- Determine uma expressão de $q$ como função afim de $p$.
- Determine uma expressão de $p$ como função afim de $q$.
Resolução >> Resolução
<< Enunciado… Ler maisUm passeio ao longo da marginal
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 38 Ex. 1
Num passeio que deu ao longo da marginal da sua cidade, o Pedro partiu de um café a $5$ km da sua residência e seguiu a caminho de casa, sempre a andar ao mesmo ritmo. Pelo seu relógio, concluiu que andou cada quilómetro em $15$ minutos.
- Complete a seguinte tabela:
Tempo, $t$, em minutos $0$ $30$ Distância do Pedro a casa, $d$, em quilómetros $4$ $0$ - Escreva uma expressão que represente a distância a que o Pedro
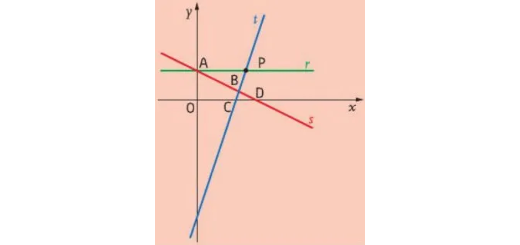
As funções afins $f$, $g$ e $h$
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 37 Ex. 6
No referencial da figura encontam-se representadas as funções afins $f$, $g$ e $h$, definidas por:
- $f\left( x \right) = 3x – 6$
- $g\left( x \right) = – 0,5x + 1,5$
- $h\left( x \right) = 1,5$
- Relacione os gráficos com as funções dadas.
- Determine os zeros de $f$ e de $g$.
- Calcule a área dos triângulos [CDB] e [ABP].
- Determine, sob a forma de intervalo, os conjuntos de valores de $x$ para os quais:
a) a função $f$
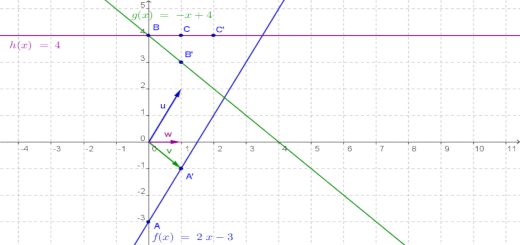
Mais retas
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 37 Ex. 2 e 3
Considere os seguintes casos de pontos e declives:
| Caso 1 | Caso 2 | Caso 3 | ||
| $A\left( {0, – 3} \right)$ e $m = 2$ | $B\left( {0,4} \right)$ e $m = – 1$ | $C\left( {1,4} \right)$ e $m = 0$ |
- Para cada caso, desenhe a reta a que pertence o ponto indicado e tem como declive o valor de $m$ apresentado. Defina as correspondentes funções afins.
- Para cada caso, defina a função afim cujo gráfico é a reta paralela
Reta a que pertencem os pontos dados
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 37 Ex. 1
Para cada alínea, represente a reta a que pertencem os pontos dados e defina a função afim cujo gráfico é a reta que desenhou.
- $A\left( {0, – 3} \right)$ e $B\left( {8,1} \right)$;
- $C\left( { – 1,0} \right)$ e $D\left( {2,6} \right)$;
- $E\left( { – 2,4} \right)$ e $F\left( {1, – 5} \right)$.
Resolução >> Resolução
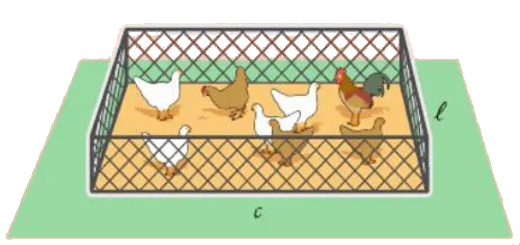
<< Enunciado… Ler maisUm galinheiro
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 29 Ex. 3
Um agricultor comprou $6$ metros de rede para fazer um galinheiro retangular, como ilustra a figura.
- Complete a seguinte tabela:
- Num referencial cartesiano, marque os pontos $\left( {c,l} \right)$ que obteve na alínea anterior.
- Explique como se pode obter os valores de $l$ à custa de $c$. Exprima $l$ em função de $c$.
- Determine o valor de c, e o correspondente valor de $l$, para o qual a área é máxima.
- Qual é a forma do galinheiro
Três funções
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 29 Ex. 2
Dadas as funções
$$\begin{array}{*{20}{c}}
{\begin{array}{*{20}{l}}
{f:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to 2x + 5}
\end{array}}&{}&{\begin{array}{*{20}{l}}
{g:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to \frac{2}{5}x + \frac{1}{5}}
\end{array}}&{}&{\begin{array}{*{20}{l}}
{h:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to 4{x^2} – 36x}
\end{array}}
\end{array}$$
- Determine a imagem de $0$, $ – 1$ e $\frac{3}{2}$ pela função $f$.
- Qual(ais) o(s) objeto(s) que tem(têm) imagem $3$ pela função $f$.
- Represente graficamente as funções dadas.
Resolução >> Resolução
<< Enunciado… Ler maisUm jardim junto a um lago
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 29 Ex. 1
Pretende-se construir um jardim junto a um lago, conforme a figura ilustra.
Três lados do jardim confinam com o lago e os outros três ficam definidos por uma rede. Pretende-se que os lados consecutivos do jardim sejam sempre perpendiculares.
As dimensões indicadas na figura estão expressas em metros. Tal como a figura mostra, $x$ é a medida em metros de um dos lados do jardim.
Vão ser utilizados, na sua totalidade, $100$ metros de rede.
- Mostre que
Calcula
Números inteiros: Matematicamente Falando 7 - Pág. 43 Ex. 3
Calcula:
- $\sqrt {16} + \sqrt 1 + \sqrt 0 $
- $12 – \sqrt {121} $
- $\sqrt {1600} + 5$
- ${\left( {\sqrt {484} } \right)^2}$
- $\sqrt[3]{{512}} + \sqrt 9 – 10$
- $\sqrt[3]{{1000}} + \sqrt[3]{{27}}$
- $\frac{{\sqrt {36} }}{3} + \frac{{18}}{{\sqrt {81} }}$
- ${\left( { – 5} \right)^2} \times {\left( { – 5} \right)^4} \times \frac{2}{{\sqrt {25} }}$
Resolução >> Resolução
<< Enunciado… Ler maisQual é o número cujo quadrado é $841$?
Números inteiros: Matematicamente Falando 7 - Pág. 43 Ex. 2
Verdadeiro ou falso?
Números inteiros: Matematicamente Falando 7 - Pág. 43 Ex. 1
Verdadeiro ou falso? Corrige as falsas.
- $2$ é a raiz quadrada de $4$.
- A raiz quadrada de um número natural é sempre um número natural.
- A raiz quadrada de $10$ é $5$.
- A raiz cúbica de um número natural é sempre um número natural.
- A raiz cúbica de $27$ é $3$.
- O quadrado de um número ímpar é par.
- O cubo de um número ímpar é ímpar.
Resolução >> Resolução
<< Enunciado… Ler maisOs carros de coleção do Pedro
Números inteiros: Matematicamente Falando 7 - Pág. 42 Ex. 9
O Pedro pretende guardar os seus carros de coleção dentro de uma caixa cúbica com $64000$ cm3 no armário do seu quarto.
Será isso possível, sabendo que a distância entre prateleiras consecutivas do armário é $37$ cm?
Explica a tua resposta.
Resolução >> Resolução
<< Enunciado… Ler mais