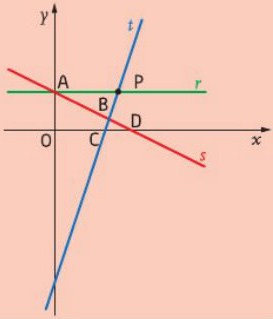
As funções afins $f$, $g$ e $h$
Funções e gráficos: Matemática A 10.º - Parte 2 - Pág. 37 Ex. 6
No referencial da figura encontam-se representadas as funções afins $f$, $g$ e $h$, definidas por:
- $f\left( x \right) = 3x – 6$
- $g\left( x \right) = – 0,5x + 1,5$
- $h\left( x \right) = 1,5$
- Relacione os gráficos com as funções dadas.
- Determine os zeros de $f$ e de $g$.
- Calcule a área dos triângulos [CDB] e [ABP].
- Determine, sob a forma de intervalo, os conjuntos de valores de $x$ para os quais:
a) a função $f$ é positiva;
b) a função $g$ é negativa;
c) $f\left( x \right) \geqslant g\left( x \right)$;
d) $f\left( x \right) < 1,5$.

$r$ → $h\left( x \right) = 1,5$$s$ → $g\left( x \right) = – 0,5x + 1,5$
$t$ → $f\left( x \right) = 3x – 6$
- Como $$f\left( x \right) = 0 \Leftrightarrow 3x – 6 = 0 \Leftrightarrow x = 2$$ e $$g\left( x \right) = 0 \Leftrightarrow – 0,5x + 1,5 = 0 \Leftrightarrow x = 3$$ então $x = 2$ é o único zero de $f$ e $x = 3$ é o único zero de $g$.
- Os pontos $C$ e $D$ são pontos de ordenada nula, pois pertencem ao eixo $Ox$.
Por outro lado, como são pontos das retas $t$ e $s$, respetivamente, as suas abcissas são os zeros das funções $f$ e $g$. Assim, $C\left( {2,0} \right)$ e $D\left( {3,0} \right)$.O ponto $B$ é a interseção das retas $s$ e $t$:
$$\begin{array}{*{20}{c}}
{\left\{ {\begin{array}{*{20}{l}}
{y = 3x – 6} \\
{y = – 0,5x + 1,5}
\end{array}} \right.}& \Leftrightarrow &{\left\{ {\begin{array}{*{20}{l}}
{3x – 6 = – 0,5x + 1,5} \\
{y = 3x – 6}
\end{array}} \right.}& \Leftrightarrow &{\left\{ {\begin{array}{*{20}{l}}
{3,5x = 7,5} \\
{y = – 0,5x + 1,5}
\end{array}} \right.}& \Leftrightarrow &{\left\{ {\begin{array}{*{20}{l}}
{x = \frac{{15}}{7}} \\
{y = \frac{3}{7}}
\end{array}} \right.}
\end{array}$$
Portanto, $B\left( {\frac{{15}}{7},\frac{3}{7}} \right)$.Assim, sendo $B’$ a projeção ortogonal do ponto $B$ sobe o eixo Ox, temos: $${A_{\left[ {CDB} \right]}} = \frac{{\overline {CD} \times \overline {BB’} }}{2} = \frac{{1 \times \frac{3}{7}}}{2} = \frac{3}{{14}}$$
- Os pontos $A$ e $P$ têm ordenada $1,5$, pois são pontos de reta $r$.
Como o ponto $A$ pertence também à reta $s$, a sua abcissa é $1,5 = – 0,5x + 1,5 \Leftrightarrow x = 0$. Logo, $A\left( {0;1,5} \right)$.
Como o ponto $P$ pertence também à reta $t$, a sua abcissa é $1,5 = 3x – 6 \Leftrightarrow x = 2,5$. Logo, $P\left( {2,5;1,5} \right)$.
Assim, sendo $B”$ a projeção ortogonal do ponto $B$ sobe a reta $r$, temos: $${A_{\left[ {ABP} \right]}} = \frac{{\overline {AP} \times \overline {BB”} }}{2} = \frac{{\frac{5}{2} \times \left( {\frac{3}{2} – \frac{3}{7}} \right)}}{2} = \frac{{\frac{5}{2} \times \left( {\frac{{21}}{{14}} – \frac{6}{{14}}} \right)}}{2} = \frac{{\frac{5}{2} \times \frac{{15}}{{14}}}}{2} = \frac{{75}}{{56}}$$
- a) $$\begin{array}{*{20}{l}}
{f\left( x \right) > 0}& \Leftrightarrow &{3x – 6 > 0} \\
{}& \Leftrightarrow &{x > 2} \\
{}& \Leftrightarrow &{x \in \left] {2, + \infty } \right[}
\end{array}$$
b) $$\begin{array}{*{20}{l}}
{g\left( x \right) < 0}& \Leftrightarrow &{ – 0,5x + 1,5 < 0} \\
{}& \Leftrightarrow &{ – 0,5x < – 1,5} \\
{}& \Leftrightarrow &{x > 3} \\
{}& \Leftrightarrow &{x \in \left] {3, + \infty } \right[}
\end{array}$$
c) $$\begin{array}{*{20}{l}}
{f\left( x \right) \geqslant g\left( x \right)}& \Leftrightarrow &{3x – 6 \geqslant – 0,5x + 1,5} \\
{}& \Leftrightarrow &{3,5x \geqslant 7,5} \\
{}& \Leftrightarrow &{x \geqslant \frac{{15}}{7}} \\
{}& \Leftrightarrow &{x \in \left[ {\frac{{15}}{7}, + \infty } \right[}
\end{array}$$
d) $$\begin{array}{*{20}{l}}
{f\left( x \right) < 1,5}& \Leftrightarrow &{3x – 6 < 1,5} \\
{}& \Leftrightarrow &{x < 2,5} \\
{}& \Leftrightarrow &{x \in \left] { – \infty ;2,5} \right[}
\end{array}$$