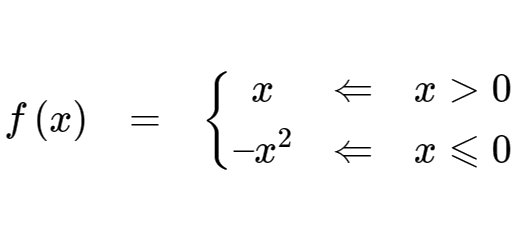
Resolva, em $\mathbb{R}$, as seguintes equações
Funções com radicais: Aleph 11 - Volume 2 Pág. 173 Ex. 11
Resolva, em $\mathbb{R}$, as seguintes equações:
- ${x^4} = 625$
- ${x^3} = – 125$
- ${x^4} + 81 = 0$
- ${x^3} – 343 = 0$
Resolução >> Resolução
<< Enunciado… Ler mais