Uma partícula move-se sobre uma reta
Derivadas: Aleph 11 - Volume 2 Pág. 88 Ex. 2
Enunciado
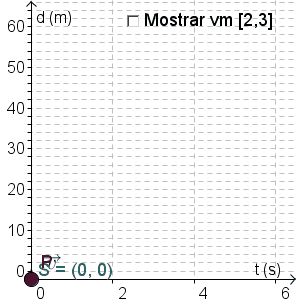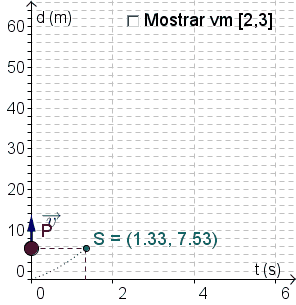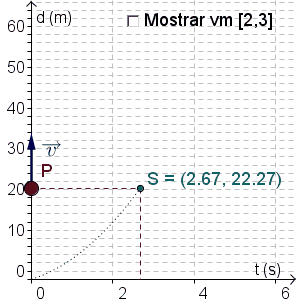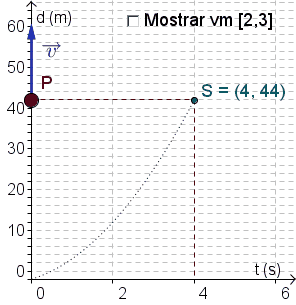Uma partícula move-se sobre uma reta de forma que, após $t$ segundos, ela encontra-se a $s\left( t \right) = 2{t^2} + 3t$ metros da sua posição inicial.
- Determine a posição da partícula após $2$ s.
- Determine a posição da partícula após $3$ s.
- Calcule a velocidade média da partícula no intervalo de tempo $\left[ {2,3} \right]$ (em segundos).
- Calcule a velocidade instantânea em $t = 2$ s.
Resolução
\[s\left( t \right) = 2{t^2} + 3t\]
- Após $2$ s, a partícula encontra-se a $s\left( 2 \right) = 2 \times {2^2} + 3 \times 2 = 14$ m da posição inicial.
- Após $3$ s, a partícula encontra-se a $s\left( 3 \right) = 2 \times {3^2} + 3 \times 3 = 27$ m da posição inicial.
- A velocidade média da partícula no intervalo de tempo $\left[ {2,3} \right]$ (em segundos) é ${v_{{m_{\left[ {2,3} \right]}}}} = \frac{{s\left( 3 \right) – s\left( 2 \right)}}{{3 – 2}} = 27 – 14 = 13$ m/s.
- A velocidade no instante $t = 2$ é $v\left( 2 \right) = s’\left( 2 \right) = 4 \times 2 + 3 = 11$ m/s, pois $s’\left( t \right) = 4t + 3$.
