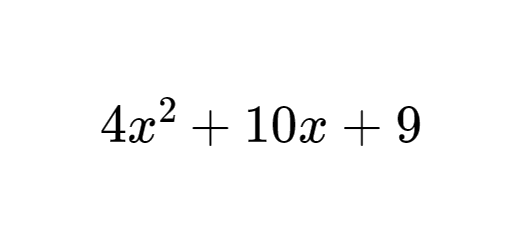A figura representa parte da representação gráfica da função $f$
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 129 Ex. 12 (Adaptado)
Enunciado
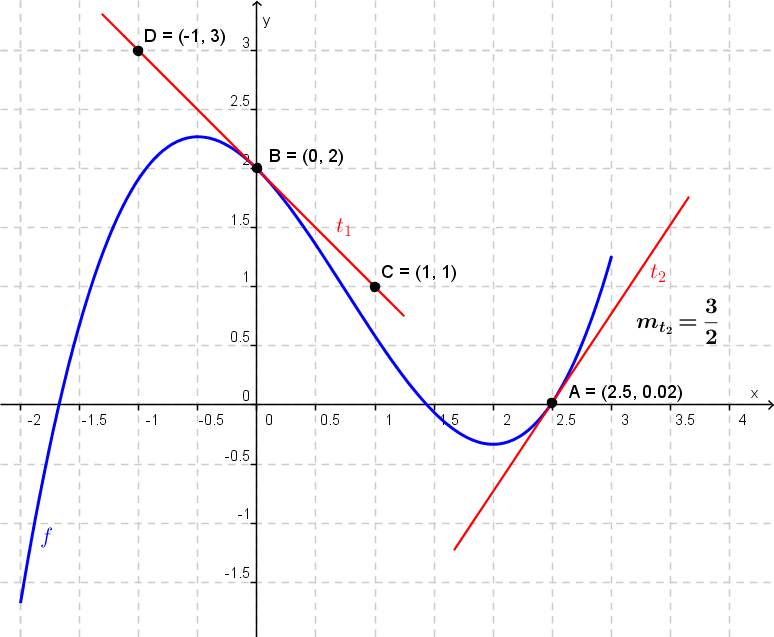A figura representa parte da representação gráfica da função $f$ derivável em $\mathbb{R}$.
As retas ${t_1}$ e ${t_2}$ são tangentes ao gráfico de $f$ nos pontos B e A, respetivamente.
Recorrendo ao gráfico:
- Resolva a equação $f'(x) = 0$ em $\left[ { – 2,3} \right]$.
- Determine o valor de $$\mathop {\lim }\limits_{x \to 2,5} \frac{{f(2,5 + h) – 0,02}}{h}$$
- Determine $f'(0)$ e a equação reduzida da reta ${t_1}$.
Resolução
Como ${x = – \frac{1}{2}}$ e ${x = 2}$ são, respetivamente, maximizante e minimizante de $f$, tem-se: $$\begin{array}{*{20}{c}}
{f'(x) = 0}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{x = – \frac{1}{2}}& \vee &{x = 2}
\end{array}}
\end{array}$$- Como a reta ${t_2}$ é tangente ao gráfico de $f$ no ponto A, tem-se: $$f'(2,5) = \mathop {\lim }\limits_{h \to 0} \frac{{f(2,5 + h) – 0,02}}{h} = {m_{{t_2}}} = \frac{3}{2}$$
- Como a reta ${t_1}$ é tangente ao gráfico de $f$ no ponto B, tem-se: $$f'(0) = {m_{{t_1}}} = \frac{{3 – 1}}{{ – 1 – 1}} = – 1$$ sendo $y = – x + 2$ a equação reduzida da reta ${t_1}$.
Nota: Ainda que o exercício esteja incluído no tema das funções trigonométricas, esclarece-se que a função $f$ é polinomial cúbica.
