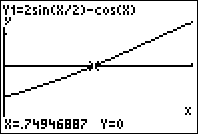$C$ é uma semicircunferência
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 129 Ex. 13
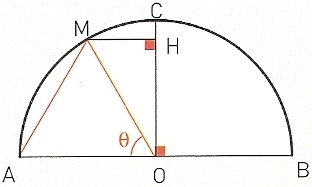$C$ é uma semicircunferência de diâmetro [AB], de centro O e de raio $r$.
[OC] é o raio perpendicular a [AB], M é um ponto do arco AC. Designa-se por $\theta $ a medida em radianos do ângulo AOM $\left( {0 \leqslant \theta \leqslant \frac{\pi }{2}} \right)$.
H é a projeção ortogonal de M sobre OC.
Existirá um ponto M tal que $\overline {AM} = \overline {MH} $?
Sugestão:
- Exprima $\overline {AM} $ e $\overline {MH} $ em função de $r$ e $\theta $.
- Estude a função $g$ definida em $\left[ {0,\frac{\pi }{2}} \right]$ por $g(\theta ) = 2\operatorname{sen} \frac{\theta }{2} – \cos \theta $ e deduza a existência de um ponto M tal que $\overline {AM} = \overline {MH} $.
- Recorrendo à calculadora gráfica, determine a amplitude de $A\widehat OM$, com aproximação às centésimas, correspondente a esta posição de M.
-
Como $$\operatorname{sen} M\widehat OH = \frac{{\overline {MH} }}{{\overline {MO} }}$$ e $$\cos M\widehat OH = \frac{{\overline {OH} }}{{\overline {MO} }}$$ vem: $$\operatorname{sen} \left( {\frac{\pi }{2} – \theta } \right) = \frac{{\overline {MH} }}{r} \Leftrightarrow \overline {MH} = r\cos \theta $$ e $$\cos \left( {\frac{\pi }{2} – \theta } \right) = \frac{{\overline {OH} }}{r} \Leftrightarrow \overline {OH} = r\operatorname{sen} \theta $$O triângulo [AOM] é isósceles, pois $\overline {OA} = \overline {OM} = r$.
Consequentemente, $$O\widehat AM = O\widehat MA = \frac{{\pi – \theta }}{2} = \frac{\pi }{2} – \frac{\theta }{2}$$Assim, e como $$\operatorname{sen} O\widehat AM = \frac{{\overline {MM’} }}{{\overline {AM} }}$$ (M’ é a projeção ortogonal de M sobre AB), vem: $$\operatorname{sen} \left( {\frac{\pi }{2} – \frac{\theta }{2}} \right) = \frac{{\overline {MM’} }}{{\overline {AM} }} \Leftrightarrow \overline {AM} = \frac{{\overline {MM’} }}{{\cos \frac{\theta }{2}}}$$Como $$\overline {MM’} = \overline {OH} = r\operatorname{sen} \theta $$ obtém-se: $$\overline {AM} = \frac{{\overline {MM’} }}{{\cos \frac{\theta }{2}}} = \frac{{r\operatorname{sen} \theta }}{{\cos \frac{\theta }{2}}} = \frac{{r\operatorname{sen} \left( {2 \times \frac{\theta }{2}} \right)}}{{\cos \frac{\theta }{2}}} = \frac{{2r\operatorname{sen} \frac{\theta }{2}\cos \frac{\theta }{2}}}{{\cos \frac{\theta }{2}}} = 2r\operatorname{sen} \frac{\theta }{2}$$
- Ora, \[\begin{array}{*{20}{l}}
{g’\left( \theta \right)}& = &{{{\left( {2\operatorname{sen} \frac{\theta }{2} – \cos \theta } \right)}^\prime }} \\
{}& = &{2 \times \frac{1}{2}\cos \frac{\theta }{2} + \operatorname{sen} \theta } \\
{}& = &{\cos \frac{\theta }{2} + \operatorname{sen} \theta }
\end{array}\]
Como $\cos \frac{\theta }{2} > 0,\forall \theta \in \left[ {0,\frac{\pi }{2}} \right]$ e $\operatorname{sen} \theta \geqslant 0,\forall \theta \in \left[ {0,\frac{\pi }{2}} \right]$, então $g'(\theta ) > 0,\forall \theta \in \left[ {0,\frac{\pi }{2}} \right]$.
Logo, a função $g$ é estritamente crescente em $\left[ {0,\frac{\pi }{2}} \right]$.Por outro lado, como $$g(0) \times g(\frac{\pi }{2}) = \left( {2\operatorname{sen} 0 – \cos 0} \right) \times \left( {2\operatorname{sen} \frac{\pi }{4} – \cos \frac{\pi }{2}} \right) = – 1 \times \sqrt 2 < 0$$ a função $g$ tem um só zero (pois é estritamente crescente) no intervalo $\left[ {0,\frac{\pi }{2}} \right]$.
Assim, existe esse ponto M, pois $$g(\theta ) = 0 \Leftrightarrow 2\operatorname{sen} \frac{\theta }{2} – \cos \theta = 0 \Leftrightarrow \overline {AM} = \overline {MH} $$ visto $r > 0$.
-
Podemos tentar uma resolução analítica da equação: $$\begin{array}{*{20}{l}}
{2\operatorname{sen} \frac{\theta }{2} – \cos \theta = 0}& \Leftrightarrow &{2\operatorname{sen} \frac{\theta }{2} – \left( {{{\cos }^2}\frac{\theta }{2} – {{\operatorname{sen} }^2}\frac{\theta }{2}} \right) = 0} \\
{}& \Leftrightarrow &{2\operatorname{sen} \frac{\theta }{2} – 1 + {{\operatorname{sen} }^2}\frac{\theta }{2} + {{\operatorname{sen} }^2}\frac{\theta }{2} = 0} \\
{}& \Leftrightarrow &{2{{\operatorname{sen} }^2}\frac{\theta }{2} + 2\operatorname{sen} \frac{\theta }{2} – 1 = 0} \\
{}& \Leftrightarrow &{\operatorname{sen} \frac{\theta }{2} = \frac{{ – 2 \pm \sqrt {4 + 8} }}{4}} \\
{}& \Leftrightarrow &{\operatorname{sen} \frac{\theta }{2} = \frac{{ – 1 \pm \sqrt 3 }}{2}} \\
{}& \Leftrightarrow &{\operatorname{sen} \frac{\theta }{2} = \frac{{ – 1 + \sqrt 3 }}{2}}
\end{array}$$
Como $0 \leqslant \theta \leqslant \frac{\pi }{2}$, vem $\theta = 2{\sin ^{ – 1}}\left( {\frac{{ – 1 + \sqrt 3 }}{2}} \right) \approx 0,75$ radianos.
