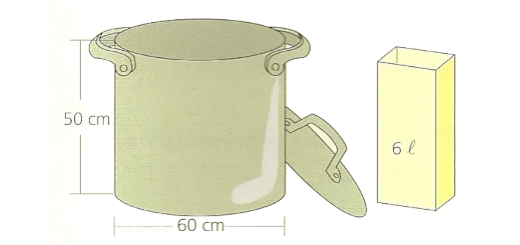
Determine uma expressão analítica da derivada de cada uma das funções

$f:x \to {e^{ – 4x}}$

$${D_f} = \mathbb{R}$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {{e^{ – 4x}}} \right)’} \\
{}& = &{\left( { – 4x} \right)'{e^{ – 4x}}} \\
{}& = &{ – 4{e^{ – 4x}}}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to  – 4{e^{ – 4x}}}
\end{array}$$

$f:x \to {e^{\sqrt {2 + x} }}$

$${D_f} = \left\{ {x \in \mathbb{R}:2 + x \geqslant 0} \right\} = \left[ { – 2, + \infty } \right[$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {{e^{\sqrt {2 + x} }}} \right)’} \\
{}& = &{\left( {\sqrt {2 + x} } \right)'{e^{\sqrt {2 + x} }}} \\
{}& = &{\frac{1}{2}{{\left( {2 + x} \right)}^{ – \tfrac{1}{2}}} \times {e^{\sqrt {2 + x} }}} \\
{}& = &{\frac{{{e^{\sqrt {2 + x} }}}}{{2\sqrt {2 + x} }}}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{\left] { – 2, + \infty } \right[ \to \mathbb{R}} \\
{}&{x \to \frac{{{e^{\sqrt {2 + x} }}}}{{2\sqrt {2 + x} }}}
\end{array}$$

$f:x \to {e^x}\left( {{x^2} + 2x + 3} \right)$

$${D_f} = \mathbb{R}$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {{e^x}\left( {{x^2} + 2x + 3} \right)} \right)’} \\
{}& = &{{e^x}\left( {{x^2} + 2x + 3} \right) + {e^x}\left( {2x + 2} \right)} \\
{}& = &{{e^x}\left( {{x^2} + 4x + 5} \right)}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to {e^x}\left( {{x^2} + 4x + 5} \right)}
\end{array}$$

$f:x \to {e^{\frac{1}{x}}} + {e^{ – \frac{1}{x}}}$

$${D_f} = \mathbb{R}\backslash \left\{ 0 \right\}$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {{e^{\frac{1}{x}}} + {e^{ – \frac{1}{x}}}} \right)}^\prime }} \\
{}& = &{ – \frac{1}{{{x^2}}}{e^{\frac{1}{x}}} + \frac{1}{{{x^2}}}{e^{ – \frac{1}{x}}}} \\
{}& = &{\frac{1}{{{x^2}}}\left( {{e^{ – \frac{1}{x}}} – {e^{\frac{1}{x}}}} \right)}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{\mathbb{R}\backslash \left\{ 0 \right\} \to \mathbb{R}} \\
{}&{x \to \frac{1}{{{x^2}}}\left( {{e^{ – \frac{1}{x}}} – {e^{\frac{1}{x}}}} \right)}
\end{array}$$

$f:x \to \frac{{{e^x} – {e^{ – x}}}}{{{e^x} + {e^{ – x}}}}$

$${D_f} = \mathbb{R}$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {\frac{{{e^x} – {e^{ – x}}}}{{{e^x} + {e^{ – x}}}}} \right)}^\prime }} \\
{}& = &{\frac{{\left( {{e^x} + {e^{ – x}}} \right)\left( {{e^x} + {e^{ – x}}} \right) – \left( {{e^x} – {e^{ – x}}} \right)\left( {{e^x} – {e^{ – x}}} \right)}}{{{{\left( {{e^x} + {e^{ – x}}} \right)}^2}}}} \\
{}& = &{\frac{{{e^{2x}} + 1 + 1 + {e^{ – 2x}} – {e^{2x}} + 1 + 1 – {e^{ – 2x}}}}{{{{\left( {{e^x} + {e^{ – x}}} \right)}^2}}}} \\
{}& = &{\frac{4}{{{{\left( {{e^x} + {e^{ – x}}} \right)}^2}}}}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to \frac{4}{{{{\left( {{e^x} + {e^{ – x}}} \right)}^2}}}}
\end{array}$$

$f:x \to \frac{x}{{{e^x}}}$

$${D_f} = \mathbb{R}$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {\frac{x}{{{e^x}}}} \right)}^\prime }} \\
{}& = &{\frac{{1 \times {e^x} – {e^x} \times x}}{{{{\left( {{e^x}} \right)}^2}}}} \\
{}& = &{\frac{{\left( {1 – x} \right){e^x}}}{{{e^{2x}}}}} \\
{}& = &{\frac{{1 – x}}{{{e^x}}}}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{\mathbb{R} \to \mathbb{R}} \\
{}&{x \to \frac{{1 – x}}{{{e^x}}}}
\end{array}$$

$f:x \to \ln \left( {3x – 5} \right)$

$${D_f} = \left\{ {x \in \mathbb{R}:3x – 5 > 0} \right\} = \left] {\frac{5}{3}, + \infty } \right[$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {\ln \left( {3x – 5} \right)} \right)’} \\
{}& = &{\frac{{\left( {3x – 5} \right)’}}{{3x – 5}}} \\
{}& = &{\frac{3}{{3x – 5}}}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{\left] {\frac{5}{3}, + \infty } \right[ \to \mathbb{R}} \\
{}&{x \to \frac{3}{{3x – 5}}}
\end{array}$$

$f:x \leftarrow x\ln x + {e^3}$

$${D_f} = \left\{ {x \in \mathbb{R}:x > 0} \right\} = {\mathbb{R}^ + }$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {x\ln x + {e^3}} \right)’} \\
{}& = &{1 \times \ln x + x \times \frac{{x’}}{x}} \\
{}& = &{\ln x + 1}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{{\mathbb{R}^ + } \to \mathbb{R}} \\
{}&{x \to \ln x + 1}
\end{array}$$

$f:x \to \ln \left( {\ln x} \right)$

$${D_f} = \left\{ {x \in \mathbb{R}:x > 0 \wedge \ln x > 0} \right\} = \left] {1, + \infty } \right[$$
$$\begin{array}{*{20}{l}}
{f'(x)}& = &{\left( {\ln \left( {\ln x} \right)} \right)’} \\
{}& = &{\frac{{\left( {\ln x} \right)’}}{{\ln x}}} \\
{}& = &{\frac{{\frac{1}{x}}}{{\ln x}}} \\
{}& = &{\frac{1}{{x\ln x}}}
\end{array}$$
$$\begin{array}{*{20}{l}}
{f’:}&{\left] {1, + \infty } \right[ \to \mathbb{R}} \\
{}&{x \to \frac{1}{{x\ln x}}}
\end{array}$$

$f:x \to \frac{{{x^2}}}{{\ln x}}$

$${D_f} = \left\{ {x \in \mathbb{R}:x > 0 \wedge \ln x \ne 0} \right\} = {\mathbb{R}^ + }\backslash \left\{ 1 \right\}$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {\frac{{{x^2}}}{{\ln x}}} \right)}^\prime }} \\
{}& = &{\frac{{2x \times \ln x – \frac{{x’}}{x} \times {x^2}}}{{{{\left( {\ln x} \right)}^2}}}} \\
{}& = &{\frac{{2x\ln x – x}}{{{{\left( {\ln x} \right)}^2}}}}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{{\mathbb{R}^ + }\backslash \left\{ 1 \right\} \to \mathbb{R}} \\
{}&{x \to \frac{{2x\ln x – x}}{{{{\left( {\ln x} \right)}^2}}}}
\end{array}$$

$f:x \to {\log _2}\left( {{x^2} – 4x} \right)$

$${D_f} = \left\{ {x \in \mathbb{R}:{x^2} – 4x > 0} \right\} = \left] { – \infty ,0} \right[ \cup \left] {4, + \infty } \right[$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {{{\log }_2}\left( {{x^2} – 4x} \right)} \right)}^\prime }} \\
{}& = &{\frac{{{{\left( {{x^2} – 4x} \right)}^\prime }}}{{\left( {{x^2} – 4x} \right)\ln 2}}} \\
{}& = &{\frac{{2x – 4}}{{\left( {{x^2} – 4x} \right)\ln 2}}}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{\left] { – \infty ,0} \right[ \cup \left] {4, + \infty } \right[ \to \mathbb{R}} \\
{}&{x \to \frac{{2x – 4}}{{\left( {{x^2} – 4x} \right)\ln 2}}}
\end{array}$$

$f:x \to {e^{3x}}\ln x$

$${D_f} = \left\{ {x \in \mathbb{R}:x > 0} \right\} = {\mathbb{R}^ + }$$
\[\begin{array}{*{20}{l}}
{f’\left( x \right)}& = &{{{\left( {{e^{3x}}\ln x} \right)}^\prime }} \\
{}& = &{3{e^{3x}} \times \ln x + {e^{3x}} \times \frac{1}{x}} \\
{}& = &{{e^{3x}}\left( {3\ln x + \frac{1}{x}} \right)}
\end{array}\]
$$\begin{array}{*{20}{l}}
{f’:}&{{\mathbb{R}^ + } \to \mathbb{R}} \\
{}&{x \to {e^{3x}}\left( {3\ln x + \frac{1}{x}} \right)}
\end{array}$$