Uma variável aleatória
Distribuição de probabilidades: Infinito 12 A - Parte 1 Pág. 104 Ex. 32
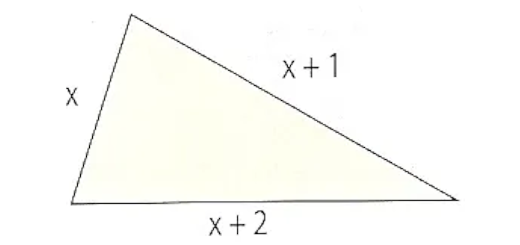
Considere a experiência aleatória de espaço de resultados S, que consiste no lançamento de dois dados perfeitos e a variável aleatória assim definida: \[\begin{array}{*{35}{l}}
X: & S\to \mathbb{R} \\
{} & (x,y)\to x\times 3y \\
\end{array}\]
 Calcule:
Calcule:
– $X((1,1))$
– $X((6,3))$
– $X((1,3))$
– $X((5,2))$e indique o contradomínio de X.
(Para facilitar, construa uma tabela de dupla entrada.)- Construa a distribuição de probabilidades desta variável aleatória.
- Calcule:
– $P(X=6)$
– $P(X=12)$
– $P(X\le 7)$
– $P(X>10)$ - Calcule o valor médio e o desvio padrão.

$x\times 3y$ $y$ 1 2 3 4 5 6 $x$ 1 3 6 9 12 15 18 2 6 12 18 24 30 36 3 9 18 27 36 45 54 4 12 24 36 48 60 72 5 15 30 45 60 75 90 6 15 36 54 72 90 108 – $X((1,1))=1\times (3\times 1)=3$
– $X((6,3))=6\times (3\times 3)=54$
– $X((1,3))=1\times (3\times 3)=9$
– $X((5,2))=5\times (3\times 2)=30$
Na tabela ao lado, apresentam-se as imagens dos resultados da experiência aleatória pela função X.
O contradomínio da função X é: \[D{{‘}_{X}}=\left\{ 3,6,9,12,15,18,24,27,30,36,45,48,54,60,72,75,90,108 \right\}\]
- Na tabela seguinte, apresenta-se a distribuição de probabilidades desta variável aleatória.
Resultados favoráveis (1,1) (1,2)
(2,1)(1,3)
(3,1)(1,4)
(2,2)
(4,1)(1,5)
(5,1)(1,6)
(2,3)
(3,2)
(6,1)(2,4)
(4,2)(3,3) (2,5)
(5,2)(2,6)
(3,4)
(4,3)
(6,2)(3,5)
(5,3)(4,4) (3,6)
(6,3)(4,5)
(5,4)(4,6)
(6,4)(5,5) (5,6)
(6,5)(6,6) $X={{x}_{i}}$ 3 6 9 12 15 18 24 27 30 36 45 48 54 60 72 75 90 108 $P(X={{x}_{i}})$ $\frac{1}{36}$ $\frac{2}{36}$ $\frac{2}{36}$ $\frac{3}{36}$ $\frac{2}{36}$ $\frac{4}{36}$ $\frac{2}{36}$ $\frac{1}{36}$ $\frac{2}{36}$ $\frac{4}{36}$ $\frac{2}{36}$ $\frac{1}{36}$ $\frac{2}{36}$ $\frac{2}{36}$ $\frac{2}{36}$ $\frac{1}{36}$ $\frac{2}{36}$ $\frac{1}{36}$ Nota: O cálculo das probabilidades resulta da aplicação da Lei de Laplace, bastando para isso ter em conta os casos favoráveis para cada valor da variável aleatória, os quais se encontram indicados imediatamente acima da tabela.
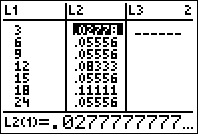
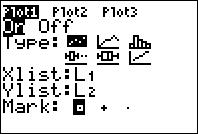
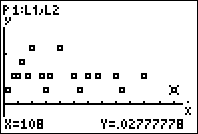
Introduzidos os valores da variável aleatória e as respetivas probabilidades em duas listas da calculadora gráfica, podemos efetuar a representação gráfica da função massa de probabilidade:
Representação gráfica da função massa de probabilidade 


-
– $P(X=6)=P(\left\{ (1,2),(2,1) \right\})=\frac{2}{36}=\frac{1}{18}$
– $P(X=12)=P(\left\{ (1,4),(2,2),(4,1) \right\})=\frac{3}{36}=\frac{1}{12}$
– $P(X\le 7)=P(X=3)+P(X=6)=P(\left\{ (1,1) \right\})+P(\left\{ (1,2),(2,1) \right\})=\frac{1}{36}+\frac{2}{36}=\frac{3}{36}=\frac{1}{12}$
– $P(X>10)=1-P(X\le 10)=1-\left[ P(X=3)+P(X=6)+P(X=9) \right]=1-(\frac{1}{36}+\frac{2}{36}+\frac{2}{36})=\frac{31}{36}$
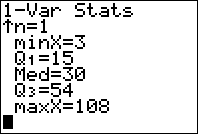
- Cálculo do valor médio e do desvio padrão:
Chamamos valor médio de uma distribuição de probabilidade ao número real $\mu $ tal que \[\mu =\sum\limits_{i=1}^{k}{({{p}_{i}}{{x}_{i}})}\]em que $k$ é o número de valores da variável aleatória, ${{x}_{i}}$ o valor da variável e ${{p}_{i}}=P(X={{x}_{i}})$ a respetiva probabilidade.
\[\mu =\frac{1}{36}\times 3+\frac{2}{36}\times 6+\frac{2}{36}\times 9+\frac{3}{36}\times 12+…+\frac{2}{36}\times 72+\frac{1}{36}\times 75+\frac{2}{36}\times 90+\frac{1}{36}\times 108=\frac{1323}{36}=\frac{147}{4}=36,75\]
Chamamos desvio padrão de uma distribuição de probabilidade ao número real $\sigma $ tal que \[\sigma =\sqrt{\sum\limits_{i=1}^{k}{{{p}_{i}}{{({{x}_{i}}-\mu )}^{2}}}}\]em que $k$ é o número de valores da variável aleatória, ${{x}_{i}}$ o valor da variável e ${{p}_{i}}=P(X={{x}_{i}})$ a respetiva probabilidade.
\[\sigma =\sqrt{\frac{1}{36}\times {{\left( 3-\frac{147}{4} \right)}^{2}}+\frac{2}{36}\times {{\left( 6-\frac{147}{4} \right)}^{2}}+…+\frac{2}{36}\times {{\left( 90-\frac{147}{4} \right)}^{2}}+\frac{1}{36}\times {{\left( 108-\frac{147}{4} \right)}^{2}}}=\sqrt{\frac{11515}{16}}=\frac{7\sqrt{235}}{4}\approx 26,83\]
 |
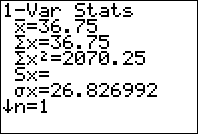 |
 |