Mais um cubo
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 186 Ex. 52
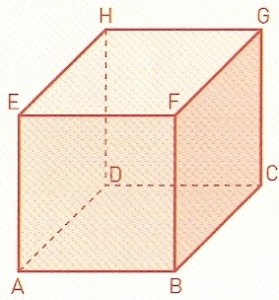Num referencial ortonormado do espaço, considere o cubo [ABCDEFGH] com 6 unidades de aresta.
A face [ABFE] é paralela ao plano zOy, a face [ABCD] é paralela ao plano xOy e $F\,(2,1,4)$.
- Mostre que o triângulo [BED] é equilátero.
- Determine uma equação cartesiana do plano que o contém.
Os lados do triângulo [BED] são diagonais faciais do cubo, logo são geometricamente iguais. Por isso, o triângulo é equilátero.
Mas, de qualquer forma…
Sendo $B\,(2,1,-2)$, $D\,(-4,-5-2)$ e $E\,(2,-5,4)$, temos:
$\overrightarrow{BE}=(0,-6,6)$, $\overrightarrow{ED}=(-6,0,-6)$ e $\overrightarrow{DB}=(6,6,0)$.
Donde, $\left\| \overrightarrow{BE} \right\|=\left\| \overrightarrow{ED} \right\|=\left\| \overrightarrow{DB} \right\|=\sqrt{{{6}^{2}}+{{6}^{2}}}=6\sqrt{2}$.
Logo, o triângulo é equilátero.
-
Comecemos por determinar um vetor normal ao plano definido pelos pontos B, E e D, isto é, um vetor $\vec{n}=(a,b,c)$ perpendicular aos vetores $\overrightarrow{BE}=(0,-6,6)$ e $\overrightarrow{ED}=(-6,0,-6)$.
Ora,
\[\begin{array}{*{35}{l}}
\left\{ \begin{array}{*{35}{l}}
\vec{n}.\overrightarrow{BE}=0 \\
\vec{n}.\overrightarrow{ED}=0 \\
\end{array} \right. & \Leftrightarrow & \left\{ \begin{array}{*{35}{l}}
(a,b,c).(0,-6,6)=0 \\
(a,b,c).(-6,0,-6)=0 \\
\end{array} \right. & \Leftrightarrow & \left\{ \begin{array}{*{35}{l}}
-6b+6c=0 \\
-6a-6c=0 \\
\end{array} \right. & \Leftrightarrow & \left\{ \begin{array}{*{35}{l}}
b=c \\
a=-c \\
\end{array} \right. \\
\end{array}\]
Logo, um vetor normal ao plano BED é, por exemplo, $\overrightarrow{{{n}_{1}}}=(-1,1,1)$.Assim, a equação pedida é da forma $-x+y+z+d=0$.
Como o ponto B pertence a esse plano, vem $-2+1-2+d=0\Leftrightarrow d=3$.Logo, $-x+y+z+3=0$ é uma equação do plano BED.
