Uma pirâmide quadrangular regular
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 187 Ex. 53
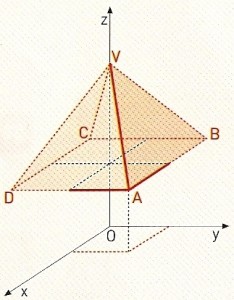Considere Oxyz um referencial ortonormado.
A pirâmide quadrangular regular está assente sobre um plano paralelo a xOy, tem o vértice no eixo Oz e os planos xOz e yOz são planos mediadores das arestas da base (como ilustra a figura).
Conhecem-se ainda $A\,(1,1,3)$ e a altura da pirâmide, que é 5 unidades.
- Caracterize, por uma condição, o plano em que a base da pirâmide está assente.
- Identifique, pelas suas coordenadas, os outros vértices da pirâmide.
- Calcule a medida do comprimento da aresta lateral da pirâmide.
- Calcule o volume da pirâmide.
- Escreva equações cartesianas da recta que contém a aresta lateral AV.
- Determine um vector normal ao plano $\alpha $ da face [ABV] e escreva uma equação desse plano.
- Considere a esfera que tem por círculo máximo o círculo circunscrito à base da pirâmide e escreva uma condição que a defina.
O plano em que a base da pirâmide está assente pode ser caracterizado pela condição $z=3$.
- Os outros vértices da pirâmide têm as seguintes coordenadas:
$B\,(-1,1,3)$, $C\,(-1,-1,3)$, $D\,(1,-1,3)$ e $V\,(0,0,8)$.
- A medida da aresta a pirâmide é:
$\overline{VA}=\sqrt{{{(1-0)}^{2}}+{{(1-0)}^{2}}+{{(3-8)}^{2}}}=\sqrt{27}=3\sqrt{3}$ unidades.
- O volume da pirâmide, em unidades cúbicas, é:
\[V=\frac{1}{3}\times \overline{AB}\times \overline{AD}\times \overline{V’V}=\frac{1}{3}\times 2\times 2\times 5=\frac{20}{3}\]
(V´é a projecção de V sobre a base da pirâmide.)
- Como $A\,(1,1,3)$ e $V\,(0,0,8)$, então $\overrightarrow{AV}=(-1,-1,5)$.
Logo, uma equação vetorial da recta AV é $(x,y,z)=(1,1,3)+k(-1,-1,5)\,,\,\,k\in \mathbb{R}$.
Desta equação resulta:
\[\begin{matrix}
\frac{x-1}{-1}=\frac{y-1}{-1}=\frac{z-3}{5} & \Leftrightarrow & -x+1=-y+1=\frac{z-3}{5} & \Leftrightarrow & \begin{matrix}
y=x & \wedge & 5y+z-8=0 \\
\end{matrix} \\
\end{matrix}\]
Logo, $\begin{matrix}
y=x & \wedge & 5y+z-8=0 \\
\end{matrix}$ são equações cartesianas da recta pedida.
- Ora, $\overrightarrow{AV}=(-1,-1,5)$ e $\overrightarrow{AB}=(-2,0,0)$.
Determinemos um vetor normal ao plano considerado, isto é, um vetor $\vec{n}=(a,b,c)$ perpendicular aos vetores $\overrightarrow{AV}=(-1,-1,5)$ e $\overrightarrow{AB}=(-2,0,0)$.
Ora,
\[\begin{array}{*{35}{l}}
\left\{ \begin{array}{*{35}{l}}
(a,b,c).(-1,-1,5)=0 \\
(a,b,c).(-2,0,0)=0 \\
\end{array} \right. & \Leftrightarrow & \left\{ \begin{array}{*{35}{l}}
-a-b+5c=0 \\
-2a=0 \\
\end{array} \right. & \Leftrightarrow & \left\{ \begin{array}{*{35}{l}}
a=0 \\
b=5c \\
\end{array} \right. \\
\end{array}\]
Logo, $\overrightarrow{{{n}_{1}}}=(0,5,1)$, por exemplo, é um vetor perpendicular ao plano ABV.Assim, o plano AVB pode ser caracterizado por uma equação da forma $5y+z+d=0$.
Como A pertence a este plano, vem $5\times 1+3+d=0\Leftrightarrow d=-8$.Logo, $5y+z-8=0$ é uma equação do plano ABV.
(Note que foi este um dos planos utilizados para definir a recta AV, na alínea anterior. Qual foi o outro plano?)
- Ora, essa esfera tem centro em $V’\,(0,0,3)$ e raio $r=\frac{\overline{BD}}{2}=\frac{2\sqrt{2}}{2}=\sqrt{2}$.
Logo, essa esfera pode ser definida pela condição ${{x}^{2}}+{{y}^{2}}+{{(z-3)}^{2}}\le 2$.
