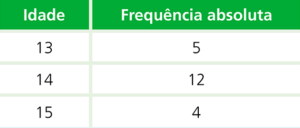
Distribuição das idades dos alunos de uma turma

A distribuição das idades dos alunos de uma turma é dada pela seguinte tabela.

1. O número de alunos da turma é:
   [A] 12        [B] 21        [C] 17        [D] 16
   pois \(n = 5 + 12 + 4 = 21\).
   
   
2. A média de idades dos alunos desta turma é:
   [A] superior a 14.
   [B] inferior a 14.
   [C] 14.
   [D] impossível de calcular.
   pois há 5 alunos com idade de 13 anos e apenas 4 com idade de 15 anos.
   
   
3. Se considerarmos a idade do professor de Matemática e calcularmos novamente a média das idades, esta será:
   [A] inferior à das idades dos alunos.
   [B] superior à das idades dos alunos.
   [C] a mesma da das idades dos alunos.
   [D] impossível de calcular.
   
   
4. A mediana das idades dos alunos é:
   [A] 13        [B] 13,5        [C] 14        [D] 15
   pois, se ordenarmos as idades por ordem crescente, identificamos que o valor que se encontra na 11.ª posição é 14.
   
   
5. A amplitude interquartil é:
   [A] 1        [B] 2        [C] 0,5        [D] 0
   pois o primeiro quartil é \({Q_1} = \frac{{{x_5} + {x_6}}}{2} = \frac{{13 + 14}}{2} = 13,5\) e o terceiro quartil é \({Q_3} = \frac{{{x_{16}} + {x_{17}}}}{2} = \frac{{14 + 14}}{2} = 14\).