Observa os seguintes gráficos
Gráficos de funções afins: Matematicamente Falando 8 - Pág. 177 Ex. 13
Enunciado
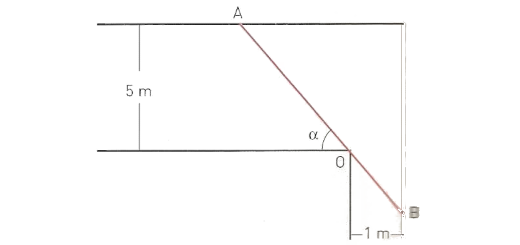
Observa os seguintes gráficos.
- Alguma das funções representadas é uma função linear?
Explica a tua resposta. - Escreve a expressão algébrica da função f.
- O que têm de comum as duas retas?
- Qual é a ordenada na origem da reta que representa a função g?
- Determina uma expressão algébrica da função g.
Resolução
Observa os seguintes gráficos.
- Sim, uma das funções representadas é uma função linear: a função f.
A função f é linear, pois o gráfico é uma reta não vertical que contém a origem do referencial. - Visto que é \(f\left( 1 \right) = 2\) o declive da reta que é o gráfico da função f, então uma expressão algébrica da função f é \(f\left( x \right) = 2x\).
- As duas retas têm igual declive.
- É \( – 2\) a ordenada na origem da reta que representa a função g, pois o ponto de coordenadas \(\left( {0, – 2} \right)\) é um ponto dessa reta.
- Uma expressão algébrica da função g é \(g\left( x \right) = 2x – 2\).