Um triângulo retângulo isósceles
Isometrias: Matematicamente Falando 8 - Pág. 115 Ex. 3
Enunciado
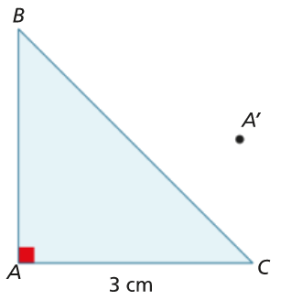O triângulo [ABC] da figura desenhada pelo João é isósceles e retângulo em A.
- Qual é a amplitude do ângulo ABC? Porquê?
- Copia e constrói as imagens B’ de B e C’ de C pela translação que transforma A em A’.
- Sem utilizar a régua e o transferidor, indica, justificando:
a) os comprimentos dos segmentos de reta [A’C’] e [A’B’];
b) a amplitude do ângulo A’C’B’;
c) como classificas o triângulo [A’B’C’].
Resolução
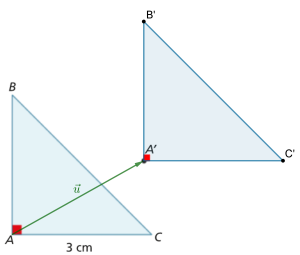
O triângulo [ABC] da figura desenhada pelo João é isósceles e retângulo em A.
- Num triângulo, a lados iguais opõem-se ângulos iguais.
Por outro lado, sabemos que a soma das amplitudes dos ângulos internos de um triângulo é igual a 180°.
Assim, \(A\widehat BC = A\widehat CB = \frac{{180^\circ – B\widehat AC}}{2} = \frac{{180^\circ – 90^\circ }}{2} = 45^\circ \). - A construção das imagens B’ de B e C’ de C, pela translação que transforma A em A’, está acima.
- As isometrias preservam a amplitude dos ângulos e as distâncias entre os pontos.
Assim, como a translação é uma isometria, temos:
a) \(\overline {A’B’} = \overline {A’C’} = \overline {AB} = \overline {AC} = 3\) cm;
b) \(A’\widehat {B’}C’ = A\widehat BC = 45^\circ \);
c) O triângulo [A’B’C’] é retângulo isósceles.
