Um octógono regular
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 60 Ex. 5
Enunciado
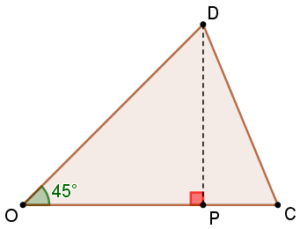
Considera um octógono regular inscrito numa circunferência de centro O e raio 4 cm e decomposto em oito triângulos de vértice O e com um lado comum ao octógono.
- Justifica que os triângulos, nos quais está dividido o octógono, são iguais e que \(C\widehat OD = 45^\circ \).
- Determina o valor exato das áreas do triângulo [OCD] e do octógono.
Resolução
Como o octógono é regular, então a circunferência está dividida em oito arcos geometricamente iguais.
Assim sendo, vem: \(C\widehat OD = \overparen{CD} = \frac{{360^\circ }}{8} = 45^\circ \).
Cada um desses triângulos possui um ângulo interno com 45 graus de amplitude (o de vértice O), como vimos anteriormente.
Por outro lado, cada um desses triângulos possui lados adjacentes a esse ângulo que são geometricamente iguais, pois são raios da mesma circunferência.
Assim, pelo critério LAL, conclui-se que esses oito triângulos, em que o octógono está dividido, são geometricamente iguais.
- Consideremos a altura do triângulo [OCD] relativa ao lado [OC], conforme ilustrado na figura ao lado.
No triângulo retângulo [OPD], vem \({\mathop{\rm sen}\nolimits} C\widehat OD = \frac{{\overline {DP} }}{{\overline {OD} }}\), donde:
\[\begin{array}{*{20}{l}}{{\mathop{\rm sen}\nolimits} 45^\circ = \frac{{\overline {DP} }}{4}}& \Leftrightarrow &{\frac{{\sqrt 2 }}{2} = \frac{{\overline {DP} }}{4}}\\{}& \Leftrightarrow &{\overline {DP} = 2\sqrt 2 }\end{array}\]
Logo, em centímetros quadrados, as áreas pedidas são:
\[\begin{array}{*{20}{l}}{{A_{\left[ {OCD} \right]}} = \frac{{\overline {OC} \times \overline {DP} }}{2} = \frac{{4 \times 2\sqrt 2 }}{2} = 4\sqrt 2 }\\{{A_{Octógono}} = 8 \times {A_{\left[ {OCD} \right]}} = 8 \times 4\sqrt 2 = 32\sqrt 2 }\end{array}\]
