Num acampamento
Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 117 Ex. 4
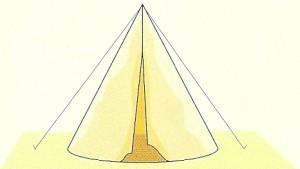Num acampamento utiliza-se uma tenda cónica, cuja base é um círculo com 4 m de diâmetro e cujo volume é 15,072 m3.
Qual é a altura da tenda?
Como o diâmetro da base é 4 m, então o raio tem 2 m de comprimento.
Como sabemos, o volume de um cone, com raio da base r e altura h, é dado por: \[{{V}_{c}}=\frac{1}{3}\times {{A}_{b}}\times h=\frac{1}{3}\times \pi \times {{r}^{2}}\times h\]
Substituindo os valores conhecidos nessa expressão, obtém-se: \[15,072=\frac{1}{3}\times \pi \times {{2}^{2}}\times h\]
Donde, \[\begin{array}{*{35}{l}}
15,072=\frac{1}{3}\times \pi \times {{2}^{2}}\times h & \Leftrightarrow & \frac{1}{3}\times \pi \times {{2}^{2}}\times h=15,072 \\
{} & \Leftrightarrow & \frac{4\pi }{3}\times h=15,072 \\
{} & \Leftrightarrow & 4\pi \times h=45,216 \\
{} & \Leftrightarrow & h=\frac{45,216}{4\pi } \\
{} & \Leftrightarrow & h=\frac{11,304}{\pi } \\
\end{array}\]
Logo, a altura da tenda é, aproximadamente, $h\simeq 3,6\,m$.
