A distância entre os automóveis
Funções com radicais: Aleph 11 - Volume 2 Pág. 177 Ex. 11
Dois automóveis circulam à mesma velocidade, em estradas perpendiculares, em direção a um cruzamento.
Um deles encontra-se a $5$ km do cruzamento e o outro a $6$ km.
Representa graficamente a função que dá a distância entre os dois automóveis à medida que se aproximam do cruzamento.
Utilizando a calculadora gráfica, determina quando é que a distância entre os automóveis é mínima.
Seja $x$ a distância, em km, percorrida por cada um dos automóveis em função do tempo.
Em cada instante (com exceção de dois [quais?]), os dois automóveis e o cruzamento definem os vértices de um triângulo retângulo de catetos com comprimentos $\left| {6 – x} \right|$ e $\left| {5 – x} \right|$, em km.
Então, em cada instante após o momento inicial (inclusive nos dois acima referidos [porquê?]), a distância, em km, entre os automóveis pode ser expressa por: \[d\left( x \right) = \sqrt {{{\left( {6 – x} \right)}^2} + {{\left( {5 – x} \right)}^2}} \]
Recorrendo à calculadora gráfica obtém-se:
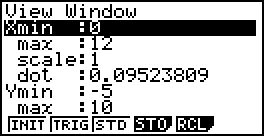 |
 |
 |
A distância entre os automóveis é mínima quando eles se encontram a $0,5$ km do cruzamento, tendo um deles passado o cruzamento e o outro ainda não o alcançou.
-
Extensão: Confirme que a distância entre os automóveis é mínima quando eles se encontram a $0,5$ km do cruzamento, considerando que a derivada da função é definida por: \[d’\left( x \right) = \frac{{2x – 11}}{{\sqrt {{{\left( {6 – x} \right)}^2} + {{\left( {5 – x} \right)}^2}} }}\]