Prove que
Funções racionais: Aleph 11 - Volume 2 Pág. 49 Ex. 11
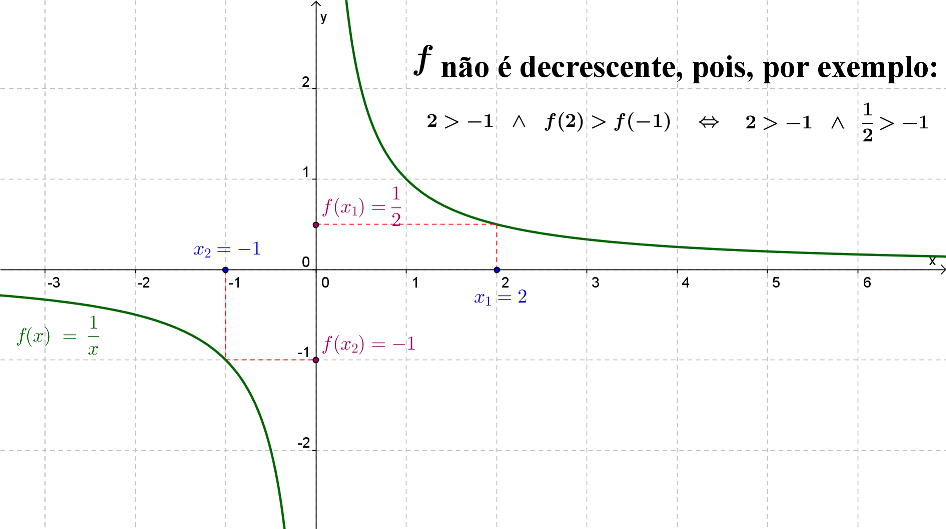
Prove que a função definida por $f\left( x \right) = \frac{1}{x}$ não é monótona no seu domínio.
A função é estritamente decrescente em ${\mathbb{R}^ – }$, quer em ${\mathbb{R}^ + }$, pois ${x_1} > {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right),\forall x \in {\mathbb{R}^ – }$ e ${x_1} > {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right),\forall x \in {\mathbb{R}^ + }$, respetivamente.
No entanto, a função não é monótona no seu domínio, pois, por exemplo, $\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{2 > – 1}& \wedge &{f\left( 2 \right) > f\left( { – 1} \right)}
\end{array}}& \Leftrightarrow &{\begin{array}{*{20}{c}}
{2 > – 1}& \wedge &{\frac{1}{2} > – 1}
\end{array}}
\end{array}$.
A função $f\left( x \right) = \frac{1}{x}$ não é decrescente
