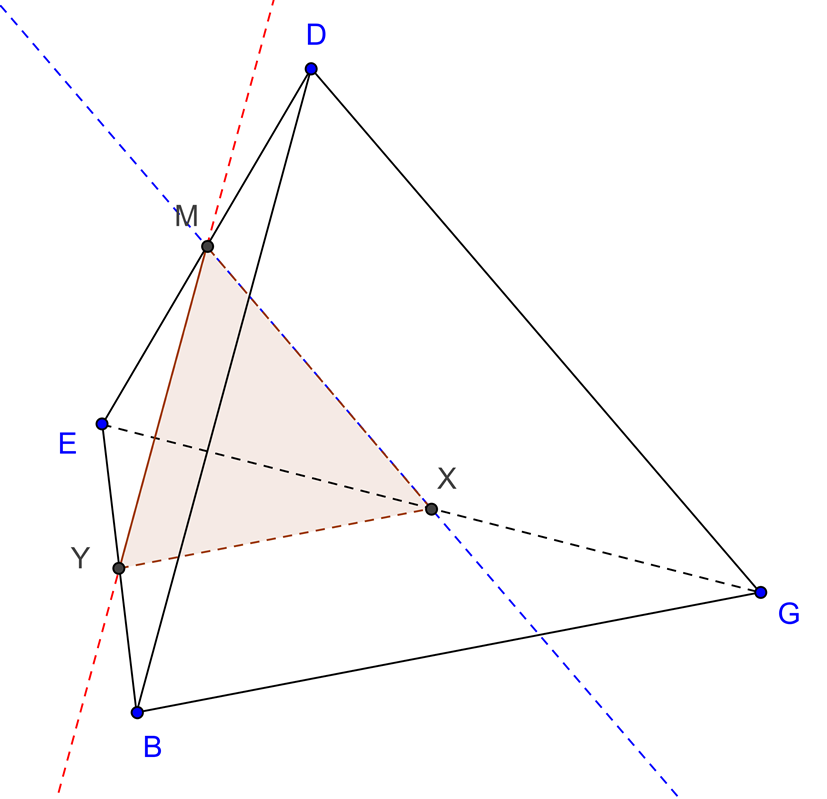
Cortes produzidos num tetraedro
Resolução de problemas de geometria: Matemática A 10.º - Parte 1 - Pág. 57 Ex. 3
Enunciado
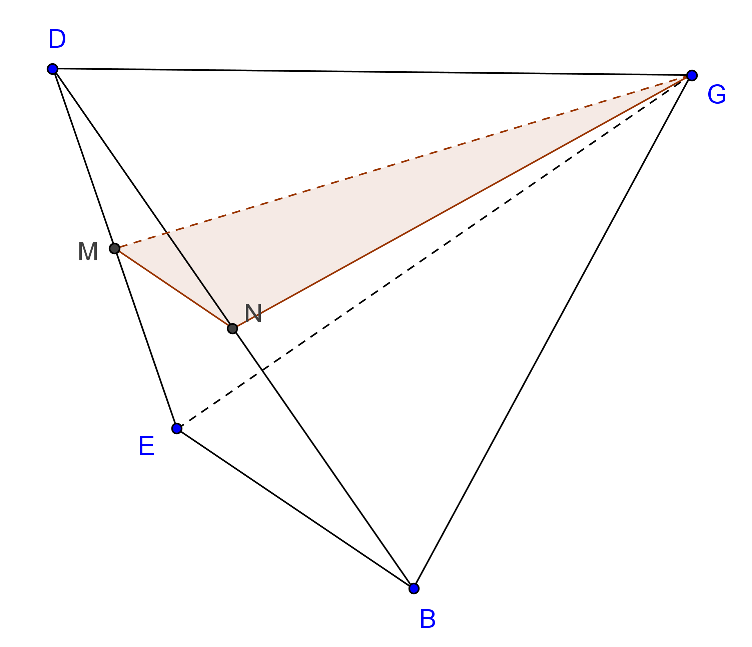
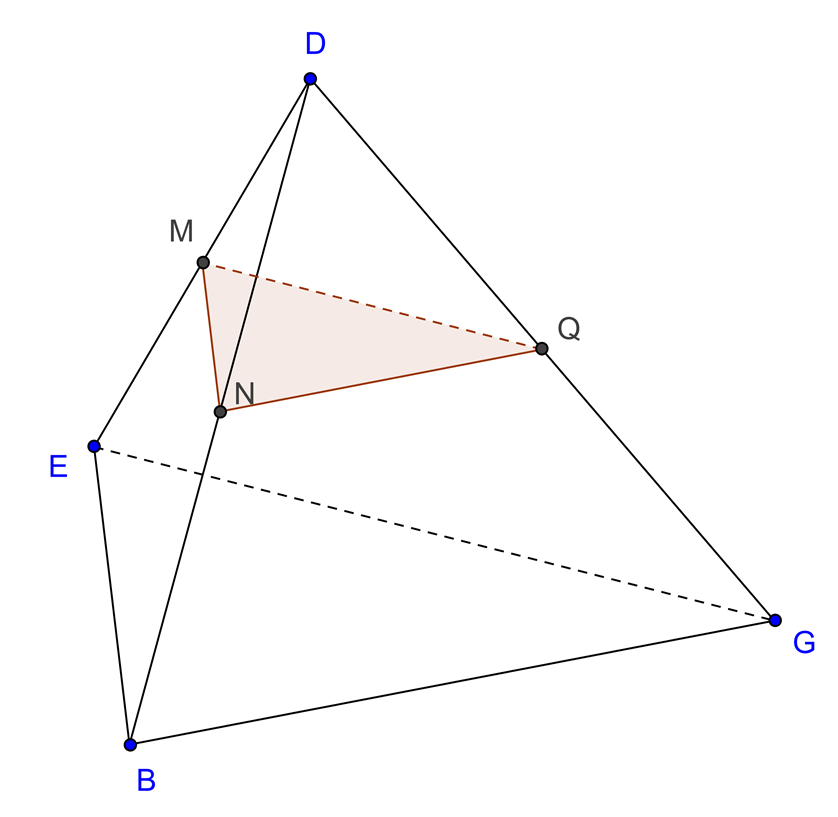
Seja [BDEG] um tetraedro regular.
Os pontos M, N e Q são pontos médios das arestas a que pertencem.
Desenhe os cortes produzidos no tetraedro pelos planos indicados.
| Plano MNG | Plano MNQ | |
 |
 |
|
| Plano que contém a reta MN e é paralelo a DG | Plano MNT, sendo $\overline {TG} = \frac{1}{4}\overline {BG} $ | |
 |
 |
|
| Plano que contém a reta UM e é paralelo a DG | Plano MBG | |
 |
 |
|
| Plano que passa em M e é paralelo a DBG | ||
 |
||
R1
| Plano MNG |
 |
| O corte produzido é o triângulo isósceles [MNG]. |
R2
| Plano MNQ |
 |
| O corte produzido é o triângulo equilátero [MNQ]. |
R3
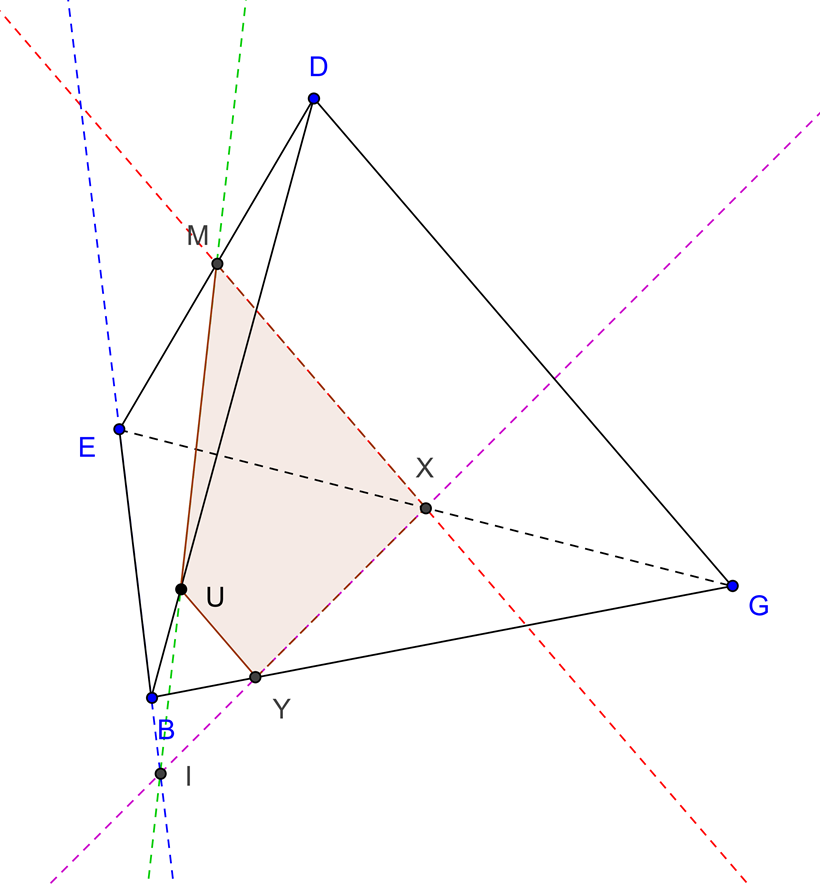
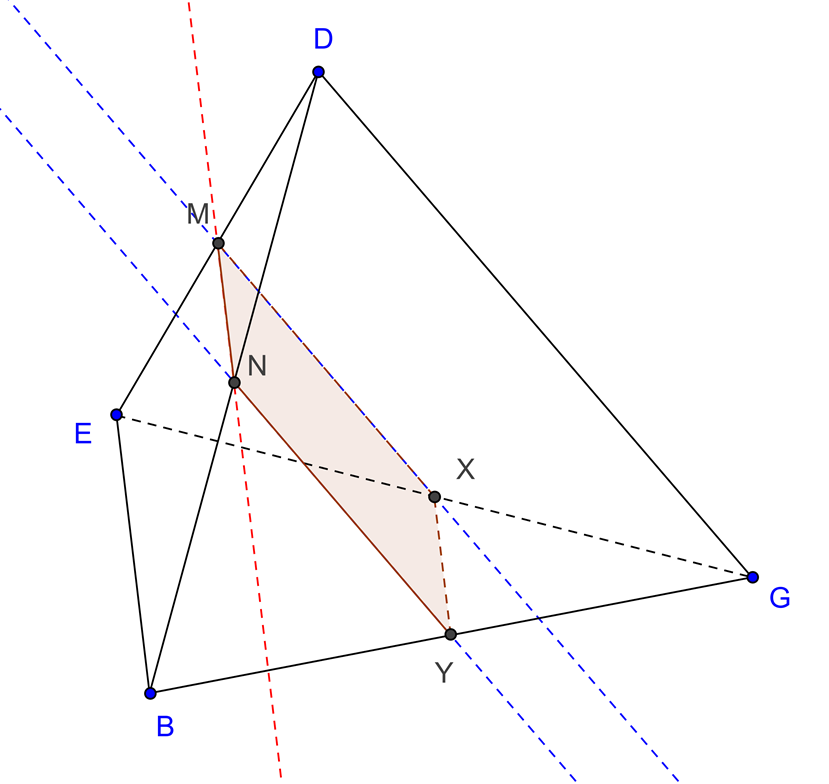
| Plano que contém a reta MN e é paralelo a DG |
 |
|
O corte produzido é o quadrado [MNYX]. $X \in EG$ e $MX\parallel DG$, $Y \in BG$ e $NY\parallel DG$. |
R4
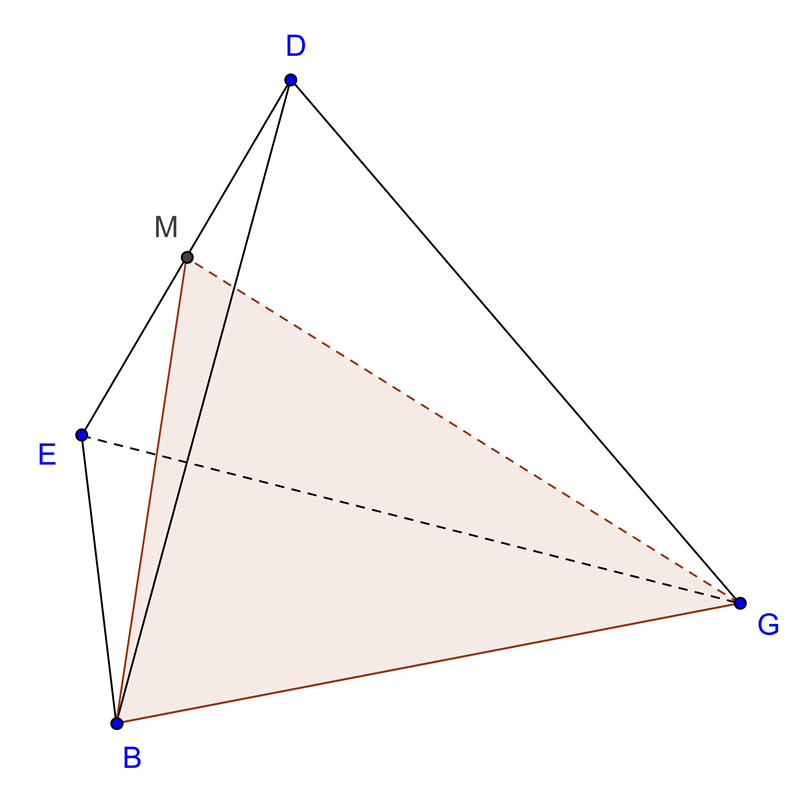
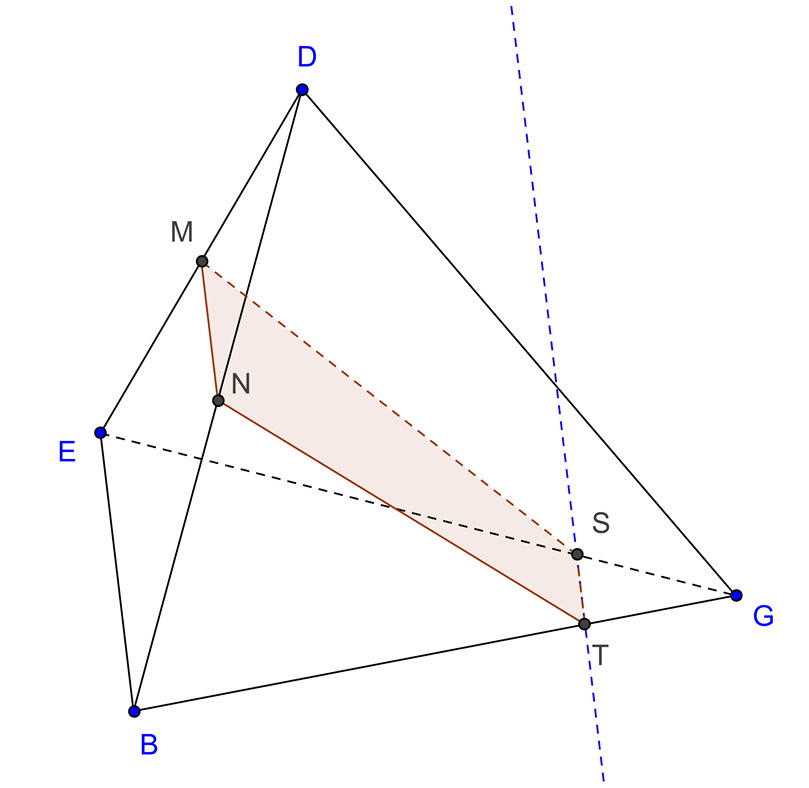
| Plano MNT, sendo $\overline {TG} = \frac{1}{4}\overline {BG} $ |
 |
|
O corte produzido é o trapézio isósceles [MNTS]. $S \in EG$ e $ST\parallel EB\parallel MN$. |
R5
| Plano que contém a reta UM e é paralelo a DG |
 |
|
O corte produzido é o quadrilátero [MUYX]. $X \in EG$ e $MX\parallel DG$. O ponto $Y \in BG$ determina-se obtendo primeiro o ponto I, ponto de intersecção das retas EB e UM. Y é o ponto de intersecção de XI com BG. |
R6
| Plano MBG |
 |
| O corte produzido é o triângulo isósceles [MBG]. |
R7
| Plano que passa em M e é paralelo a DBG |
 |
|
O corte produzido é o triângulo equilátero [MXY]. $X \in EG$ e $MX\parallel DG$. $Y \in BE$ e $MY\parallel BD$. |
