A Casinha da Matemática Blog
Análise combinatória: Infinito 12 A - Parte 1 Pág. 177 Ex. 59
Enunciado
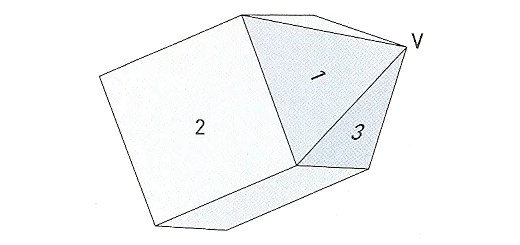
Na figura está representado um poliedro com nove faces, que pode ser decomposto num cubo e numa pirâmide quadrangular regular.
Pretende-se numerar as nove faces do poliedro com os números de 1 a 9 (um número diferente em cada face).
Como se vê na figura, três das faces do poliedro já estão numeradas, com os números 1, 2 e 3.
- De quantas maneiras diferentes podemos numerar as outras seis faces, com os restantes seis números?
- Com os
…
Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 177 Ex. 58
Enunciado
O alfabeto Morse utiliza os símbolos • e –.
Utilizando no máximo três destes símbolos, quantas sequências distintas se podem obter?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 177 Ex. 57
Enunciado
Pretende-se dispor, numa prateleira de uma estante, oito livros todos distintos, dois dos quais são de Inglês.
De quantas maneiras diferentes o podemos fazer, de tal forma que os dois livros de Inglês fiquem juntos?
Resolução >>
Resolução
<< Enunciado…
Ler mais
O Sol ilumina aproximadamente metade do planeta Terra o tempo inteiro. Mas por que quando ele vai embora, o céu fica escuro? As outras estrelas e todo o resto do universo não deviam brilhar no céu inteiro e, consequentemente, iluminar tudo por aqui? Neste programa do ABC da Astronomia, você vai entender melhor os mistérios que envolvem a noite, o intervalo de tempo entre o por do Sol e seu nascimento no horizonte. Vai saber também como que a resposta … Ler mais
Astro mais próximo da Terra a nosso único satélite natural, a Lua é muito mais do que inspiradora de poemas. Mais de dez homens já estiveram por lá em uma série de seis missões que levaram três anos. Neste programa do ABC da Astronomia, você descobre como se deu a colisão que deu origem à Lua e aprende como é a relação entre o satélite natural e o planeta Terra. A nossa força da gravidade faz com que a Lua … Ler mais
As três leis de Kepler são aplicáveis a todos os sistemas binários de astros e aos novos sistemas solares que estão sendo descobertos. A busca da harmonia que norteou o seu trabalho talvez seja o que mantenha suas leis aceitas até hoje. Além de ser um dos nomes mais ligados à teoria do Heliocentrismo, Kepler participou do processo de ruptura de uma tradição de mais de 15 séculos, que até então associava as figuras esféricas à perfeição. Neste programa, você … Ler mais
Ele é muito grande: tem massa equivalente a 2,5 vezes a massa de todos os outros planetas do Sistema Solar juntos. Mas quando temos a experiência de olhar para ele no telescópio pela primeira vez é que dá aquele estalo de que somos mesmo muito pequenos, apenas uma bolinha girando em torno do Sol. Neste programa do ABC da Astronomia, você conhece um Júpiter, este gigante formado por gases e líquidos que tem mais de 60 luas ao redor e … Ler mais
A luz visível traz muita informação do universo, mas ela é apenas uma pequena parcela de todas as radiações que já detectamos no universo: as estrelas e os astros emitem muito mais informações do que nós somos capazes de ver a olho nu, ou mesmo com a ajuda de telescópios. É a partir daí que nasce a Astronomia do Invisível, que você vai conhecer neste programa. Esta vertente da astronomia está em busca de mais segredos escondidos nas micro-ondas, raios … Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 176 Ex. 56
Enunciado
Num saco existem doze cartões de igual forma e material, dos quais quatro são verdes, quatro são azuis e quatro são pretos.
Para cada uma das cores, os cartões estão numerados de 1 a 4.
- Retirando do saco, um a um, todos os cartões e dispondo-os em fila, qual é a probabilidade dos cartões com os mesmos algarismos ficarem todos juntos?
Apresente o resultado na forma de fração irredutível.
- Suponha que se retiraram do saco alguns cartões.
…
Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 176 Ex. 55
Enunciado
Seis amigos chegam à escola conduzindo cada um a sua motorizada e encontram os dez lugares do parque de estacionamento vazios.
- De quantas formas podem estacionar as motorizadas se não houver qualquer restrição?
- Supondo que os lugares de estacionamento lhes foram atribuídos ao acaso, qual a probabilidade de ficarem todos juntos, num dos extremos do estacionamento?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Binómio de Newton: Infinito 12 A - Parte 1 Pág. 176 Ex. 54
Enunciado
- Escreva todos os subconjuntos do conjunto $A=\left\{ d,e,f \right\}$.
(Não esqueça que o conjunto vazio e o conjunto A são subconjuntos de A.)
- Transcreva e complete o quadro seguinte e compare-o com as 5 primeiras linhas do Triângulo de Pascal.
Número de subconjuntos de B com:
| Subcomjuntos de B |
0 elementos |
1 elementos |
2 elementos |
3 elementos |
4 elementos |
Total |
| $\left\{ {} \right\}$ |
1 |
– |
– |
– |
– |
$1={{2}^{0}}$ |
| $\left\{ a \right\}$ |
1 |
1 |
– |
– |
– |
…
Ler mais
Binómio de Newton: Infinito 12 A - Parte 1 Pág. 176 Ex. 53
Enunciado
Escreva sob a forma de polinómio as expressões:
- ${{(2+x)}^{4}}$
- ${{(1-2x)}^{5}}$
- ${{(\sqrt{2}+x)}^{6}}$
- ${{(\sqrt{2}x-\sqrt{3})}^{4}}$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 175 Ex. 52
Enunciado
Um grupo de doze rapazes e oito raparigas pretende organizar um clube.
- De quantos modos diferentes se pode obter uma direção de cinco elementos com funções indiferenciadas, sabendo que:
a) são todos elegíveis;
b) é formada só por rapazes;
c) é formada só por raparigas;
d) é formada por 3 rapazes e duas raparigas?
- Sabendo que a escolha dos elementos para a direção é feita por sorteio e que todos são elegíveis, qual a probabilidade:
a) dos
…
Ler mais
Análise combinatória: Infinito 12 A - Parte 1 Pág. 175 Ex. 51
Enunciado
Um autocarro chega à fronteira com 30 passageiros. Destes 30 passageiros, 10 levam contrabando.
O funcionário da alfândega vai vistoriar 8 passageiros escolhidos ao acaso.
Qual é a probabilidade de dois e só dois dos passageiros com contrabando sejam escolhidos? (Apresente o resultado aproximado às milésimas.)
Resolução >>
Resolução
<< Enunciado…
Ler mais