Um projétil é lançado do cimo de uma ponte
Cálculo diferencial: Infinito 12 A - Parte 2 Pág. 215 Ex. 50
Um projétil é lançado do cimo de uma ponte, para o alto.
A sua altura $y$, acima do solo, em metros, $t$ segundos depois é dada por:$$y = f(t) = – 5{t^2} + 15t + 12$$
- Qual é a altura da ponte?
- Qual é a velocidade média do projétil durante o 1.º segundo? E no 2.º?
- Qual é a velocidade do projétil, quando $t=1$? E quando $t=2$?
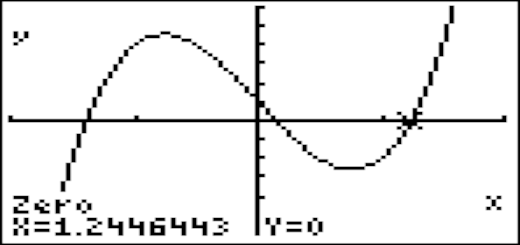
Como interpreta os resultados? - Ao fim de quanto tempo o


















![Uma corda [BC]](https://www.acasinhadamatematica.pt/wp-content/uploads/2018/03/9V2Pag60-2a-720x340.png)




