Tagged: taxa média de variação
Cálculo diferencial: Infinito 12 A - Parte 2 Pág. 228 Ex. 91
Enunciado
Uma piza foi confecionada à temperatura de 230º C e retirada do forno às 17 horas para um compartimento que se encontra à temperatura de 20º C.
Admita que, passados 5 minutos, a piza se encontra à temperatura de 150º C.
Sabe-se que a temperatura $A$ (em ºC) de arrefecimento de um corpo varia com o tempo $t$ (em minutos), decorridos após ser retirado da fonte de calor, de acordo com uma lei do tipo $$A(t) = … Ler mais
Cálculo diferencial: Infinito 12 A - Parte 2 Pág. 212 Ex. 40
Enunciado
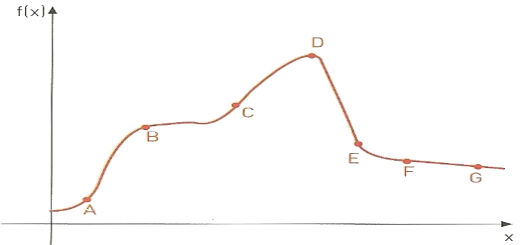
Com referência ao gráfico da função $f$ representada na figura, indique:
- entre que par de pontos consecutivos a taxa média de variação da função é maior.
- entre que par de pontos consecutivos a taxa média de variação está mais próxima de zero.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Teoria de limites: Infinito 12 A - Parte 2 Pág. 207 Ex. 21
Enunciado
Dadas as funções reais de variável real, assim definidas:$$\begin{array}{*{20}{c}}
{f(x) = {x^2} + 1}&{\text{e}}&{g(x) = \frac{1}{x}}
\end{array}$$
- Determine, em função de $h$, a taxa média de variação de cada uma das funções no intervalo $\left[ {1,1 + h} \right]$, com $h > 0$.
- Calcule se existir:
a) $\mathop {\lim }\limits_{h \to 0} \frac{{f(1 + h) – f(1)}}{h}$
b) $\mathop {\lim }\limits_{h \to 0} \frac{{g(1 + h) – g(1)}}{h}$
c) $\mathop {\lim }\limits_{h \to 0} \frac{{f(a
…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 193 Ex. 32
Enunciado
O perímetro $P$ de um círculo de raio $r$ é dado pela expressão $P=2\pi r$.
- Calcule a taxa média de variação de $P$ em cada um dos intervalos: $\left[ 2,9 \right]$, $\left[ 2;2,5 \right]$, $\left[ 2;2,1 \right]$, $\left[ 2;2,001 \right]$ e $\left[ 2,2+h \right]$.
- Qual é o valor da taxa de variação do perímetro para $r=2$?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 193 Ex. 31
Enunciado
Um estudo sobre audiências televisivas concluiu que, durante os 90 minutos da transmissão do jogo França-Portugal, do Campeonato da Europa de Futebol, em 2000, a variação do número de telespectadores, no nosso país, foi modelada, aproximadamente, pela função definida por:
\[E(t)=-0,04t+10-\frac{49}{t+10}\]
Em que $E$ representa o número de telespectadores (em milhões) e $t$ o tempo (em minutos).
- Qual o número de pessoas que assistiu ao fim da transmissão?
- Calcule as taxas médias de variação do número de
…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 192 Ex. 30
Enunciado
Seja $f$ uma função polinomial e $h$ um número real positivo.
Calcule a taxa média de variação de $f$ no intervalo $\left[ x,x+h \right]$, nos casos seguintes:
- $f(x)=-3{{x}^{2}}+7x-5$
- $f(x)={{x}^{3}}-3x+1$
- $f$ é uma função afim
- $f$ é uma função constante.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Derivadas: Infinito 11 A - Parte 2 Pág. 192 Ex. 29
Enunciado
- Dada a função afim $f$: $x\to 3x+5$, calcule a taxa média de variação nos intervalos $\left[ -3,-2 \right]$ e $\left[ -1,3 \right]$.
- Repita o exercício anterior para a função $g$: $x\to {{x}^{2}}+2x$.
Resolução >>
Resolução
<< Enunciado…
Ler mais