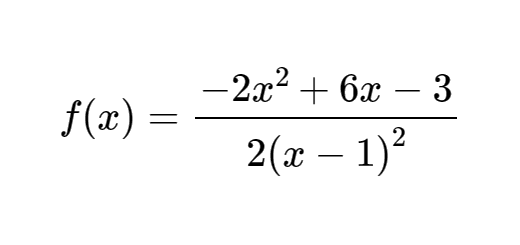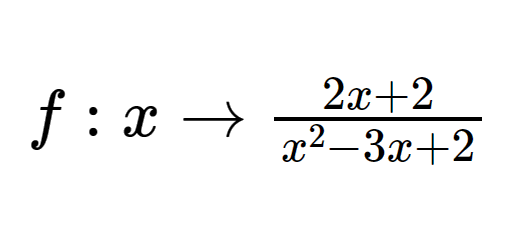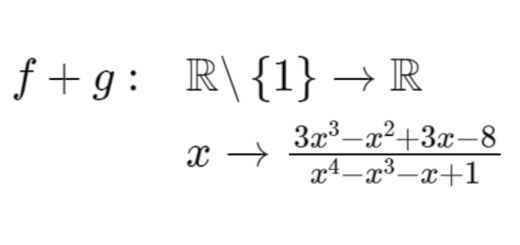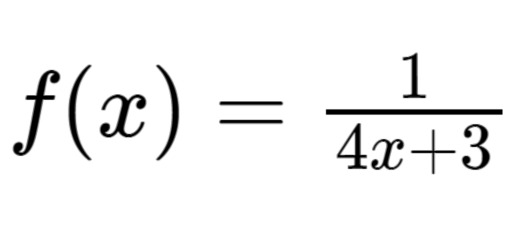Tagged: operações com funções
Mais funções: Aleph 11 - Volume 2 Pág. 139 Ex. 14
Enunciado
Mostre que as funções seguintes são iguais.
\[\begin{array}{*{20}{c}}
{\begin{array}{*{20}{c}}
{f:}&{\mathbb{R}\backslash \left\{ { – 3,3} \right\} \to \mathbb{R}} \\
{}&{x \to \frac{{x – 3}}{{{x^2} – 9}}}
\end{array}}&{}&{\text{e}}&{}&{\begin{array}{*{20}{c}}
{g:}&{\mathbb{R}\backslash \left\{ { – 3,3} \right\} \to \mathbb{R}} \\
{}&{x \to \frac{1}{{x + 3}}}
\end{array}}
\end{array}\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Mais funções: Aleph 11 - Volume 2 Pág. 139 Ex. 12
Enunciado
As funções de Heaviside e rampa são definidas, respetivamente, por: \[\begin{array}{*{20}{c}}
{H\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
0& \Leftarrow &{x < 0} \\
{\frac{1}{2}}& \Leftarrow &{x = 0} \\
1& \Leftarrow &{x > 0}
\end{array}} \right.}&{\text{e}}&{R\left( x \right) = \left\{ {\begin{array}{*{20}{c}}
0& \Leftarrow &{x \leqslant 0} \\
x& \Leftarrow &{x > 0}
\end{array}} \right.}
\end{array}\]
Mostre que:
- $R\left( x \right) = x\,H\left( x \right)$
- $R\left( x \right) = \frac{{x + \left| x \right|}}{2}$
- $\left( {R \circ R}
…
Ler mais
Funções com radicais: Infinito 11 A - Parte 2 Pág. 206 Ex. 81
Enunciado
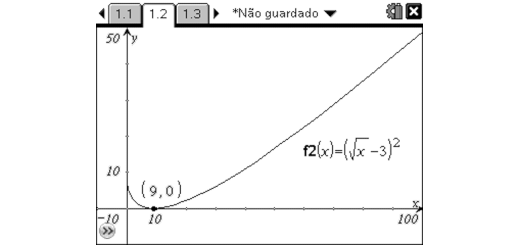
Considere as funções reais de variável real assim definidas: \[\begin{matrix}
f:x\to {{(\sqrt{x}+3)}^{2}} & \text{e} & g:x\to {{(\sqrt{x}-3)}^{2}} \\
\end{matrix}\]
- Determine o domínio de f e de g.
- Determine, se existirem, os zeros de f e de g.
- Caracterize as funções $(f+g)$ e $(f\times g)$ e apresente as expressões de $(f+g)(x)$ e $(f\times g)(x)$ na forma mais simplificada possível.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 60
Enunciado
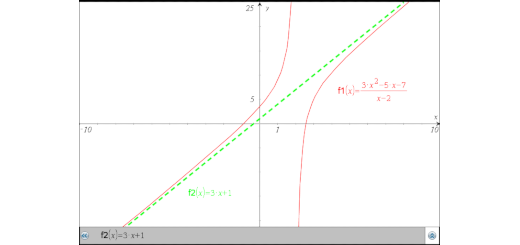
- Determine os números reais a, b e c tais que: \[\frac{3{{x}^{2}}-5x-7}{x-2}=ax+b+\frac{c}{x-2}\]
- Conjecture se o gráfico da função racional definida por \[f(x)=\frac{3{{x}^{2}}-5x-7}{x-2}\] tem uma assimptota oblíqua e, no caso afirmativo, indique a sua equação.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 59
Enunciado
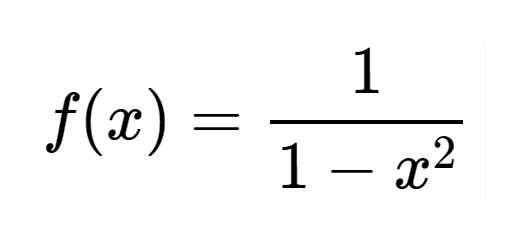
f é uma função racional definida em $\mathbb{R}\backslash \left\{ -1,1 \right\}$ por \[f(x)=\frac{1}{1-{{x}^{2}}}\]
Encontre os reais a e b tais que, para todo o $x\ne 1\wedge x\ne -1$, \[f(x)=\frac{a}{1-x}+\frac{b}{1+x}\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 58
Enunciado
f é uma função racional definida em $\mathbb{R}\backslash \left\{ 1 \right\}$ por \[f(x)=\frac{-2{{x}^{2}}+6x-3}{2{{(x-1)}^{2}}}\]
Encontre os reais a, b e c tais que, para todo o $x\ne 1$, \[f(x)=a+\frac{b}{x-1}+\frac{c}{2{{(x-1)}^{2}}}\]
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 57
Enunciado
Sejam \[\begin{matrix}
f:x\to \frac{2x+2}{{{x}^{2}}-3x+2} & e & g:x\to \frac{4x-4}{x-2} \\
\end{matrix}\]
- Mostre que $f\times g$ e $\frac{f}{g}$ são funções racionais e determine o seu domínio.
- Determine os valores de x tais que $f(x)\le \frac{1}{2}$.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 56
Enunciado
Sejam: \[\begin{matrix}
f:x\to \frac{3x-4}{{{(x-1)}^{2}}} & e & g:x\to \frac{4}{{{x}^{3}}-1} \\
\end{matrix}\]
Mostre que $f+g$ é uma função racional e determine o seu domínio.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Operações com funções: Infinito 11 A - Parte 2 Pág. 200 Ex. 55
Enunciado
Sejam as funções racionais definidas por: \[\begin{matrix}
f(x)=\frac{1}{4x+3} & e & g(x)=\frac{2x-1}{(4x+3)(x-7)} \\
\end{matrix}\]
- Indique o seu domínio.
- Caracterize $f+g$.
- Determine $x\in \mathbb{R}$ tal que $f(x)\le g(x)$.
Resolução >>
Resolução
<< Enunciado…
Ler mais