A secção de um túnel
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 128 Ex. 8
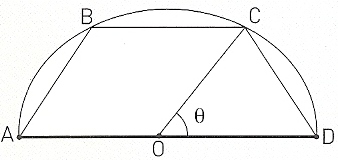A secção de um túnel é um semicírculo com 1 hm de raio.
No interior do túnel há uma estrutura com a forma de um trapézio, como mostra a figura.
Qual é o valor de $\theta $ $\left( {0 < \theta < \frac{\pi }{2}} \right)$ que torna máxima a área da secção da estrutura trapezoidal?
Seja $C’$ a projeção ortogonal do ponto C sobre [AD].
Ora, $$\operatorname{sen} \theta = \frac{{\overline {CC’} }}{{\overline {OC} }} \Leftrightarrow \overline {CC’} = \overline {OC} \times \operatorname{sen} \theta $$ e $$\cos \theta = \frac{{\overline {OC’} }}{{\overline {OC} }} \Leftrightarrow \overline {OC’} = \overline {OC} \times \cos \theta $$
Como $\overline {OC} = 1$, vem: $\overline {CC’} = \operatorname{sen} \theta $ e $\overline {OC’} = \cos \theta $.
Assim, a área da estrutura trapezoidal é dada por: $$\begin{array}{*{20}{l}}
{A\left( \theta \right)}& = &{\frac{{\overline {AD} + \overline {BC} }}{2} \times \overline {CC’} } \\
{}& = &{\frac{{2 + 2\cos \theta }}{2} \times \operatorname{sen} \theta } \\
{}& = &{\operatorname{sen} \theta + \operatorname{sen} \theta \times \cos \theta }
\end{array}$$ com ${0 < \theta < \frac{\pi }{2}}$.
Como $$\begin{array}{*{20}{l}}
{A’\left( \theta \right)}& = &{\left( {\operatorname{sen} \theta + \operatorname{sen} \theta \times \cos \theta } \right)’} \\
{}& = &{\cos \theta + {{\cos }^2}\theta – {{\operatorname{sen} }^2}\theta } \\
{}& = &{\cos \theta + {{\cos }^2}\theta – \left( {1 – {{\cos }^2}\theta } \right)} \\
{}& = &{2{{\cos }^2}\theta + \cos \theta – 1}
\end{array}$$ com ${0 < \theta < \frac{\pi }{2}}$, então $$\begin{array}{*{20}{l}}
{A’\left( \theta \right) = 0}& \Leftrightarrow &{2{{\cos }^2}\theta + \cos \theta – 1 = 0 \wedge 0 < \theta < \frac{\pi }{2}} \\
{}& \Leftrightarrow &{\cos \theta = \frac{{ – 1 \pm \sqrt {1 + 8} }}{4} \wedge 0 < \theta < \frac{\pi }{2}} \\
{}& \Leftrightarrow &{\cos \theta = \frac{{ – 1 \pm 3}}{4} \wedge 0 < \theta < \frac{\pi }{2}} \\
{}& \Leftrightarrow &{\left( {\cos \theta = 1 \vee \cos \theta = \frac{1}{2}} \right) \wedge 0 < \theta < \frac{\pi }{2}} \\
{}& \Leftrightarrow &{\theta = \frac{\pi }{3}}
\end{array}$$
Assim, temos:
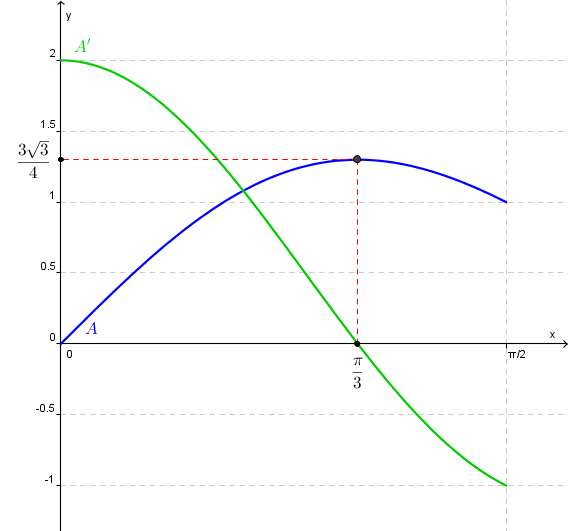
| $\theta $ | $0$ | ${\frac{\pi }{3}}$ | ${\frac{\pi }{2}}$ | ||
| $A’\left( \theta \right) = 2{\cos ^2}\theta + \cos \theta – 1$ | $+$ | $0$ | $-$ | ||
| Variação de $A$ | $ \nearrow $ | ${\frac{{3\sqrt 3 }}{4}}$ | $ \searrow $ |
$$\begin{array}{*{20}{l}}
{A\left( {\frac{\pi }{3}} \right)}& = &{\operatorname{sen} \frac{\pi }{3} + \operatorname{sen} \frac{\pi }{3} \times \cos \frac{\pi }{3}} \\
{}& = &{\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{1}{2}} \\
{}& = &{\frac{{3\sqrt 3 }}{4}}
\end{array}$$
Portanto, a área é máxima para ${\theta = \frac{\pi }{3}}$.
Sobre o preenchimento da tabela relativamente ao sinal de $A’$:
Como $2{\cos ^2}0 + \cos 0 – 1 = 2 + 1 – 1 = 2 > 0$ e $2{\cos ^2}\frac{\pi }{2} + \cos \frac{\pi }{2} – 1 = 0 + 0 – 1 = – 1 < 0$ e dado que a função $x \to 2{\cos ^2}x + \cos x – 1$ é contínua em $\mathbb{R}$, esta não pode mudar de sinal sem anular.
