Partes dos gráficos de duas funções, novamente
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 117 Ex. 12
Enunciado
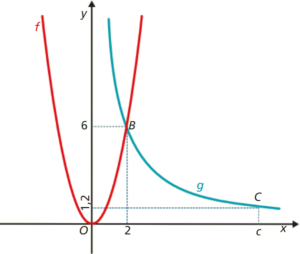Na figura, estão representadas, num referencial cartesiano, partes dos gráficos de duas funções, f e g.
Sabe-se que:
- a função f é uma função quadrática definida por \(f\left( x \right) = a{x^2}\), sendo a um número positivo;
- a função g é uma função de proporcionalidade inversa;
- o ponto B pertence ao gráfico da função f e ao gráfico da função g e tem coordenadas \(\left( {2,\;6} \right)\);
- o ponto C pertence ao gráfico da função g e tem coordenadas \(\left( {c;\;1,2} \right)\), sendo c um número positivo.
- Qual e o valor de \(f\left( { – 2} \right)\)?
[A] \( – 6\) [B] \(6\) [C] \( – 4\) [D] \(4\) - Qual é o valor de c?
Mostra como chegaste à tua resposta.
Resolução
Na figura, estão representadas, num referencial cartesiano, partes dos gráficos de duas funções, f e g.
Sabe-se que:
-
a função f é uma função quadrática definida por \(f\left( x \right) = a{x^2}\), sendo a um número positivo;
-
a função g é uma função de proporcionalidade inversa;
-
o ponto B pertence ao gráfico da função f e ao gráfico da função g e tem coordenadas \(\left( {2,\;6} \right)\);
-
o ponto C pertence ao gráfico da função g e tem coordenadas \(\left( {c;\;1,2} \right)\), sendo c um número positivo.
- Ora, \(f\left( { – 2} \right) = a \times {\left( { – 2} \right)^2} = a \times {\left( { + 2} \right)^2} = f\left( 2 \right) = 6\).
Logo, a alternativa correta é a [B].
- Como a função g é uma função de proporcionalidade inversa, será do tipo \(x \times y = k\), com k constante e real. Como o ponto B é um ponto do gráfico de g, então \(\begin{array}{*{20}{c}}{2 \times 6 = k}& \Leftrightarrow &{k = 12}\end{array}\). Logo, a função g pode ser definida por \(g\left( x \right) = \frac{{12}}{x}\).
Finalmente, como C é um ponto do gráfico de g, temos:\[\begin{array}{*{20}{l}}{g\left( c \right) = 1,2}& \Leftrightarrow &{\frac{{12}}{c} = 1,2}\\{}& \Leftrightarrow &{c = 10}\end{array}\]
