Um poliedro de nove faces
Análise combinatória: Infinito 12 A - Parte 1 Pág. 177 Ex. 60
Enunciado
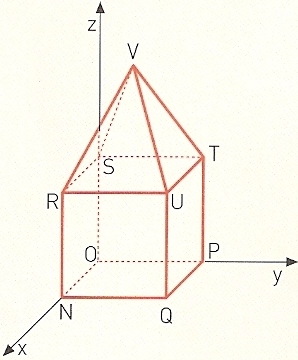Considere, agora, o poliedro do problema anterior num referencial o. n. Oxyz, de tal forma que:
- o vértice O coincida com a origem do referencial;
- o vértice N pertença ao semieixo positivo Ox;
- o vértice P pertença ao semieixo positivo Oy.
- Escolhendo, ao acaso, três dos nove vértices do sólido representado, qual é a probabilidade de pertencerem à mesma face?
- Dois amigos escolheram cada um, em segredo, um dos nove vértices do sólido.
Qual é a probabilidade dos vértices escolhidos pertencerem ambos ao plano $y=x$?
Resolução
Dos nove vértices, podem ser selecionados três deles de $NCP={}^{9}{{C}_{3}}=84$ maneiras diferentes.
Relativamente às faces triangulares do sólido, existem ${{N}_{1}}=4\times {}^{3}{{C}_{3}}=4\times 1=4$ casos favoráveis, um por face.
Relativamente às faces quadrangulares, existem ${{N}_{2}}=5\times {}^{4}{{C}_{3}}=5\times 4=20$ casos favoráveis, 4 por face.
Logo, a probabilidade pedida é $$p=\frac{4+20}{84}=\frac{2}{7}$$
- Os vértices que pertencem ao plano de equação $y=x$ são: O, Q, U, V e S.
Nada impede que os amigos possam escolher o mesmo vértice. Portanto, o número de casos favoráveis é $NCF={}^{5}A{{‘}_{2}}={{5}^{2}}=25$.
O número de casos possíveis é $NCP={}^{9}A{{‘}_{2}}=81$.
Logo, a probabilidade pedida é $$p=\frac{{}^{5}A{{‘}_{2}}}{{}^{9}A{{‘}_{2}}}=\frac{25}{81}$$
