Um domínio plano
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 182 Ex. 33
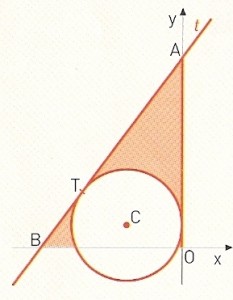Na figura está representado um referencial o. m. Oxy.
- A circunferência de centro C é tangente ao eixo das ordenadas e à reta t, em T.
- O ponto C tem coordenadas (-5,2).
- A abcissa de T é -9.
- Prove que a ordenada de T é 5.
- Prove que a equação reduzida da reta t é $y=\frac{4}{3}x+17$.
- Determine a amplitude dos ângulos agudos do triângulo [ABO] e apresente o resultado aproximado às centésimas.
- Escreva uma condição que defina a região colorida da figura (contorno incluído).
Como a circunferência é tangente ao eixo das ordenadas, esse ponto de tangência é $R(0,2)$.
Assim, o raio da circunferência é $r=\overline{CR}=5$.
Como T é outro ponto da circunferência, então:
$$\begin{array}{*{35}{l}}
\overline{TC}=5 & \Leftrightarrow & \sqrt{{{(-5+9)}^{2}}+{{(2-y)}^{2}}}=5\wedge y>0 \\
{} & \Leftrightarrow & {{(y-2)}^{2}}+16=25\wedge y>0 \\
{} & \Leftrightarrow & {{(y-2)}^{2}}=9\wedge y>0 \\
{} & \Leftrightarrow & (y=5\vee y=-1)\wedge y>0 \\
{} & \Leftrightarrow & y=5 \\
\end{array}$$Logo, a ordenada de T é 5.
- Designado por $P(x,y)$ um ponto genérico da reta t, tem-se $\overrightarrow{TP}.\overrightarrow{TC}=0$, pois uma reta tangente a uma circunferência é perpendicular ao raio nesse ponto de tangência.
Assim, vem: \[\begin{array}{*{35}{l}}
\overrightarrow{TP}.\overrightarrow{TC}=0 & \Leftrightarrow & (x+9,y-5).(-5+9;2-5)=0 \\
{} & \Leftrightarrow & 4x+36-3y+15=0 \\
{} & \Leftrightarrow & y=\frac{4}{3}x+17 \\
\end{array}\]Logo, a equação reduzida da reta t é $y=\frac{4}{3}x+17$.
- A amplitude do ângulo ABO é igual à inclinação da reta t.
Logo, \[O\hat{A}B=t{{g}^{1}}({{m}_{t}})=t{{g}^{1}}(\frac{4}{3})\simeq 53,13{}^\text{o}\]Como os ângulos OBA e OAB são complementares, será $O\hat{A}B=90{}^\text{o}-O\hat{A}B\simeq 36,87{}^\text{o}$.
-
Uma condição que define a região colorida da figura (contorno incluído) é: \[\begin{matrix}
{{(x+5)}^{2}}+{(y-2)}^{2}\ge 25 & \wedge & y\le \frac{4}{3}x+17 & \wedge & x\le 0 & \wedge & y\ge 0 \\
\end{matrix}\]
