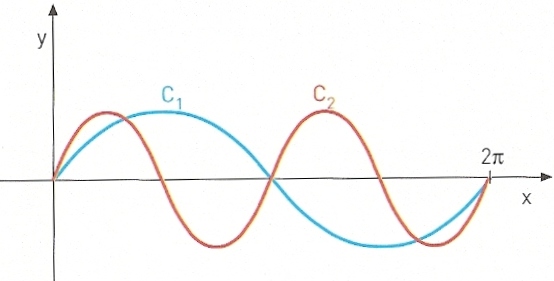
As curvas ${C_1}$ e ${C_2}$ são as representações gráficas das funções $f$ e $g$
Funções seno, co-seno e tangente: Infinito 12 A - Parte 3 Pág. 130 Ex. 14
As curvas ${C_1}$ e ${C_2}$ da figura são as representações gráficas das funções $f$ e $g$ definidas, em $\left[ {0,2\pi } \right]$, respetivamente, por:
$$\begin{array}{*{20}{c}}
{f(x) = \operatorname{sen} x}&{}&{\text{e}}&{}&{g(x) = \operatorname{sen} 2x}
\end{array}$$
- Determine as coordenadas dos pontos de intersecção das duas curvas.
- Resolva graficamente as inequações:a) $f(x) – g(x) \geqslant 0$
b) $f(x) + g(x) \geqslant 0$
c) $f(x) \times g(x) < 0$
- Indique o contradomínio da restrição da função $g$ ao intervalo $\left] {\frac{\pi }{6},\frac{{2\pi }}{3}} \right]$.
- Como $$\begin{array}{*{20}{l}}
{f(x) = g(x)}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{\operatorname{sen} x = \operatorname{sen} 2x}& \wedge &{0 \leqslant x \leqslant 2\pi }
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{\begin{array}{*{20}{l}}
{2x = x + 2k\pi }& \vee &{2x = \pi – x + 2k\pi ,k \in \mathbb{Z}}
\end{array}}& \wedge &{0 \leqslant x \leqslant 2\pi }
\end{array}} \\
{}& \Leftrightarrow &{\begin{array}{*{20}{l}}
{\begin{array}{*{20}{l}}
{x = 2k\pi }& \vee &{x = \frac{\pi }{3} + \frac{{2k\pi }}{3},k \in \mathbb{Z}}
\end{array}}& \wedge &{0 \leqslant x \leqslant 2\pi }
\end{array}} \\
{}& \Leftrightarrow &{x \in \left\{ {0,\frac{\pi }{3},\pi ,\frac{{5\pi }}{3},2\pi } \right\}}
\end{array}$$ as coordenadas dos pontos de intersecção das duas curvas são:
$$\begin{array}{*{20}{l}}
{O\left( {0,0} \right)}&;&{A\left( {\frac{\pi }{3},\operatorname{sen} \frac{\pi }{3}} \right) = \left( {\frac{\pi }{3},\frac{{\sqrt 3 }}{2}} \right)}&;&{B\left( {\pi ,0} \right)}&;&{C\left( {\frac{{5\pi }}{3}, – \frac{{\sqrt 3 }}{2}} \right)}&{\text{e}}&{D\left( {2\pi ,0} \right)}
\end{array}$$

- a)
$$\begin{array}{*{20}{l}}
{f(x) – g(x) \geqslant 0}& \Leftrightarrow &{x \in \left[ {\frac{\pi }{3},\pi } \right] \cup \left[ {\frac{{5\pi }}{3},2\pi } \right]}
\end{array}$$b)
$$\begin{array}{*{20}{l}}
{f(x) + g(x) \geqslant 0}& \Leftrightarrow &{f(x) \geqslant – g(x)} \\
{}& \Leftrightarrow &{x \in \left[ {0,\pi – \frac{\pi }{3}} \right] \cup \left[ {\pi ,\pi + \frac{\pi }{3}} \right] \cup \left\{ {2\pi } \right\}} \\
{}& \Leftrightarrow &{x \in \left[ {0,\frac{{2\pi }}{3}} \right] \cup \left[ {\pi ,\frac{{4\pi }}{3}} \right] \cup \left\{ {2\pi } \right\}}
\end{array}$$c)
$$\begin{array}{*{20}{l}}
{f(x) \times g(x) < 0}& \Leftrightarrow &{x \in \left] {\frac{\pi }{2},\pi } \right[ \cup \left] {\pi ,\frac{{3\pi }}{2}} \right[}
\end{array}$$ - Tendo em conta o gráfico e dado que $$\begin{array}{*{20}{l}}
{g(\frac{\pi }{6}) = \operatorname{sen} \left( {\frac{{2\pi }}{3}} \right) = \frac{{\sqrt 3 }}{2}}&;&{g(\frac{\pi }{4}) = \operatorname{sen} \left( {\frac{\pi }{2}} \right) = 1}&{\text{e}}&{g(\frac{{2\pi }}{3}) = \operatorname{sen} \left( {\frac{{4\pi }}{3}} \right) = – \frac{{\sqrt 3 }}{2}}
\end{array}$$ conclui-se que o contradomínio da restrição da função $g$ ao intervalo $\left] {\frac{\pi }{6},\frac{{2\pi }}{3}} \right]$ é $D’ = \left[ { – \frac{{\sqrt 3 }}{2},1} \right]$.