A Casinha da Matemática Blog
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 65 Ex. 11
Enunciado
Considera os polinómios:
| $A=7{{x}^{2}}-2x+\frac{1}{2}$ |
$B={{x}^{2}}-4x$ |
$C=3{{x}^{2}}-4x+\frac{7}{3}$ |
$D=3{{x}^{2}}+\frac{1}{2}x-\frac{2}{3}$ |
Determina e indica o grau de cada polinómio obtido:
- $A+B$
- $B-C$
- $C-D$
- $A-(B+C+D)$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 64 Ex. 8
Enunciado
Considera as seguintes expressões:
| (I) |
(II) |
(III) |
(IV) |
(V) |
(VI) |
| $2x+3y$ |
$-\frac{5}{3}$ |
$a$ |
$\frac{3}{2}a$ |
$\frac{2}{3}+x$ |
$et$ |
- Indica as que são monómios.
- De entre os monómios da alínea anterior, indica os que são semelhantes.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações de grau superior ao 1.º: Matematicamente Falando 8 - Parte 2 Pág. 64 Ex. 7
Enunciado
Copia e completa:
| Monómio |
Parte literal |
Coeficiente |
Grau |
| $3{{x}^{6}}$ |
|
|
|
| $-a$ |
|
|
|
| $\frac{x}{2}$ |
|
|
|
| $abc$ |
|
|
|
| $-2$ |
|
|
|
| $\frac{-y}{3}$ |
|
|
|
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 1.º grau: Matematicamente Falando 8 - Parte 2 Pág. 61 Ex. 6
Enunciado
Resolve cada um das equações em ordem a x e a y:
- $x+3y=5$
- $\frac{3x+y}{2}=3$
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 1.º grau: Matematicamente Falando 8 - Parte 2 Pág. 61 Ex. 5
Enunciado
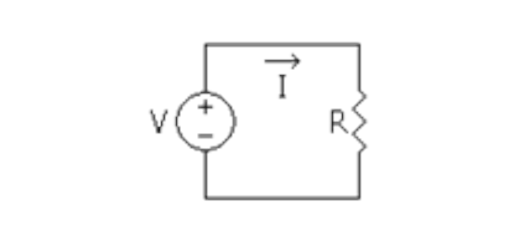
Num circuito elétrico, a diferença de potencial (V) entre dois pontos está relacionada com a intensidade da corrente que o percorre (I) e com a resistência do circuito (R), segundo a fórmula $V=RI$.
Resolve esta equação:
- em ordem a R;
- em ordem a I.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 1.º grau: Matematicamente Falando 8 - Parte 2 Pág. 58 Ex. 1
Enunciado
A relação entre graus Celsius e graus Fahrenheit é a seguinte: \[\frac{F-32}{9}=\frac{C}{5}\]
- Resolve a equação em ordem a F.
- Resolve a equação em ordem a C.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Equações do 1.º grau: Matematicamente Falando 8 - Parte 2 Pág. 59 Ex. 6
Enunciado
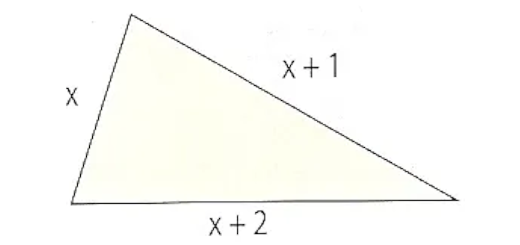
Considera o triângulo da figura (medidas expressas em centímetros).
- Escreve uma equação que te permita calcular o perímetro P do triângulo.
- Obtiveste em 1. uma equação com duas variáveis, P e x, resolvida em ordem a P.
Resolve-a em ordem a x.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Lugares geométricos: Matematicamente Falando 8 - Parte 2 Pág. 43 Ex. 5
Enunciado
O filho da Rita partiu um prato.
Com régua e compasso, tenta reconstruir o desenho do prato inteiro.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Lugares geométricos: Matematicamente Falando 8 - Parte 2 Pág. 43 Ex. 4
Enunciado
Desenha uma circunferência e assinala dois pontos, P e Q.
- Determina os pontos da circunferência que são equidistantes de P e Q.
- A Ana diz que “a mediatriz duma corda tem sempre que passar pelo centro da circunferência”.
Achas que a Ana tem razão? Porquê?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Lugares geométricos: Matematicamente Falando 8 - Parte 2 Pág. 43 Ex. 3
Enunciado
Desenha um triângulo retângulo [ABC], cujos catetos medem, respetivamente, 3 cm e 4 cm.
Desenha a circunferência circunscrita.
Quanto mede o raio desta circunferência?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Lugares geométricos: Matematicamente Falando 8 - Parte 2 Pág. 43 Ex. 2
Enunciado
Escolhe dois pontos, A e B.
Determina os pontos que distam, simultaneamente, 2 cm de A e 3 cm de B.
Quantas soluções tem o problema?
Discute os diferentes casos possíveis.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Estatística: Matematicamente Falando 8 - Parte 2 Pág. 19 Ex. 6
Enunciado
De acordo com os dados da tabela abaixo, constrói um pictograma utilizando o símbolo:
Cada símbolo representa 4 bolas.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Estatística: Matematicamente Falando 8 - Parte 2 Pág. 19 Ex. 5
Enunciado
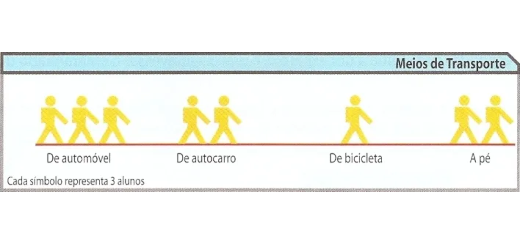
O gráfico abaixo indica os meios de transporte utilizados pelos alunos de uma turma para se deslocarem de casa à escola.
- Qual é o meio de transporte mais utilizado pelos alunos?
- Quantos alunos vão de autocarro para a escola?
- Quantos alunos tem esta turma?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Estatística: Matematicamente Falando 8 - Parte 2 Pág. 18 Ex. 4
Enunciado
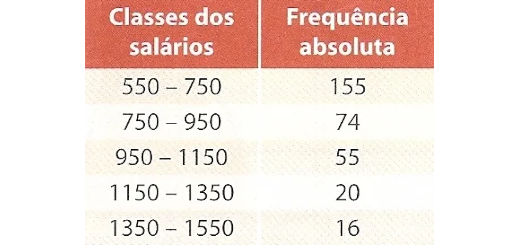
Os salários, em euros, dos empregados de uma empresa foram afixados e organizados como mostra a tabela ao lado.
- Qual a amplitude de cada classe?
- Quantos empregados têm um salário inferior a 950 euros?
- Qual a percentagem de funcionários com salário superior ou igual a 750 euros e inferior a 1350 euros?
- Elabora um histograma e o respetivo polígono de frequência desta distribuição.
Resolução >>
Resolução
<< Enunciado…
Ler mais