A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Tagged: Geometria

0

Do espaço ao plano / Aplicando / 8.º Ano

Constrói o triângulo

Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 94 Ex. 1

Enunciado

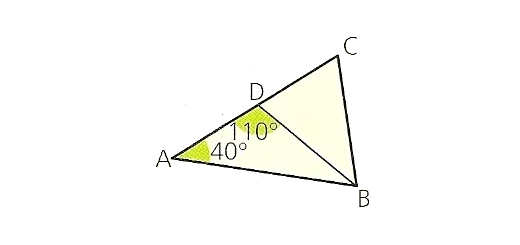
Considera o triângulo [ABC] em que:

  • $\overline{AB}=4\,cm$
  • $\widehat{A}=32{}^\text{o}$
  • $\widehat{B}=128{}^\text{o}$
  1. Constrói o triângulo.
  2. Classifica-o quanto aos lados e quanto aos ângulos.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Do espaço ao plano

Dois triângulos

Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 93 Ex. 3

Enunciado

Na figura, tem-se:

  • o ângulo de vértice C e o ângulo CDB são geometricamente iguais;
  • $\widehat{A}=40{}^\text{o}$;
  • $A\widehat{D}B=110{}^\text{o}$.
  1. Determina $B\widehat{D}C$ e $D\widehat{B}A$.
  2. Mostra que os triângulos [ABC] e [BCD] são isósceles e indica os lados iguais em cada um. Justifica convenientemente a resposta.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Do espaço ao plano

Um tetraedro

Do espaço ao plano: Matematicamente Falando 7 - Parte 2 Pág. 87 Ex. 7

Enunciado

Na figura está representado um tetraedro.

  1. Existem planos paralelos? E retas paralelas?
  2. Indica um plano que contenha a reta AD.
  3. Indica duas retas concorrentes.
  4. Está assinalado na figura um ponto que pertence a todas as faces laterais do tetraedro. Qual é esse ponto?
  5. Indica dois planos concorrentes e diz qual é a intersecção desses planos.
  6. Indica duas retas não complanares.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Vídeo / Matemática

Conjectura de Poincaré – Geometria para Entender o Universo

Uma palestra de Marcelo Viana
Marcelo Viana

Marcelo Viana nasceu no Rio de Janeiro em 1962.

Realizou os estudos em Portugal, tendo obtido a licenciatura em Matemática pela Universidade do Porto, em 1984. Regressou ao Brasil onde obteve o grau de doutor em Sistemas Dinâmicos pelo IMPA – Instituto Nacional de Matemática Pura e Aplicada do Rio de Janeiro, em 1990.

Actualmente é Investigador Catedrático e Director Adjunto do IMPA, Bolseiro de Produtividade do CNPq-Brasil, Coordenador Científico da União Matemática da América Latina (UMALCA) e … Ler mais