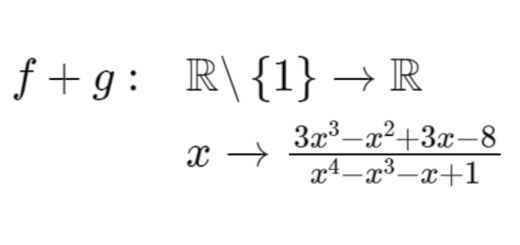Efetue
Números complexos: Infinito 12 A - Parte 3 Pág. 70 Ex. 35
Enunciado
Efetue:
- ${3i\left( {2 + 4i} \right)}$
- ${\left( {3 + 2i} \right)\left( { – 5 – i} \right)}$
- ${{{\left( {2 – 3i} \right)}^2}}$
Resolução
- Ora,
$$\begin{array}{*{20}{l}}
{3i\left( {2 + 4i} \right)}& = &{3i \times 2 + 3i \times 4i} \\
{}& = &{6i + 12{i^2}} \\
{}& = &{ – 12 + 6i}
\end{array}$$ - Ora,
$$\begin{array}{*{20}{l}}
{\left( {3 + 2i} \right)\left( { – 5 – i} \right)}& = &{ – 15 – 3i – 10i – 2{i^2}} \\
{}& = &{ – 15 – 13i + 2} \\
{}& = &{ – 13 – 13i}
\end{array}$$ - Ora,
$$\begin{array}{*{20}{l}}
{{{\left( {2 – 3i} \right)}^2}}& = &{4 – 12i + 9{i^2}} \\
{}& = &{4 – 12i – 9} \\
{}& = &{ – 5 – 12i}
\end{array}$$