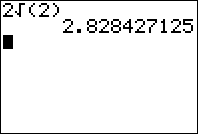A Patrícia, usando o GeoGebra
Funções com radicais: Infinito 11 A - Parte 2 Pág. 209 Ex. 99
Enunciado
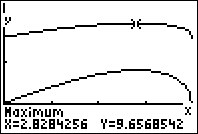
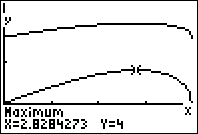
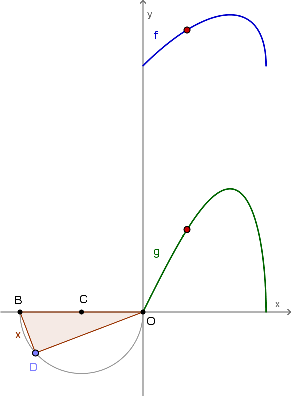A Patrícia, usando o GeoGebra, construiu os gráficos das funções perímetro e área do triângulo [OBD], como mostra a figura.
O ponto D é um ponto móvel sobre a semicircunferência, cujo diâmetro mede 4 cm, e x é o comprimento de [BD].
- A Patrícia esqueceu-se de identificar as funções.
Qual da funções, f ou g, é o perímetro e qual delas é a área?
Identifique-as, usando argumentos baseados na figura. - Escreva as correspondentes expressões analíticas e, recorrendo a uma tabela obtida na calculadora, indique os valores de x para os quais cada uma das funções é máxima.
Resolução
- Quando o ponto D tende a coincidir com o ponto B e quando tende a coincidir com o ponto O, isto é, quando $x\to 0$ e quando $x\to 4$, a área tende para zero e o perímetro tende para 8.
Logo, f é uma representação gráfica do perímetro e g uma representação gráfica da área.
- Como $\overline{OD}=\sqrt{16-{{x}^{2}}}$, o perímetro e a área, em centímetros quadrados, são dados, respetivamente, por:
$f(x)=4+x+\sqrt{16-{{x}^{2}}}\,,\,x\in \left] 0,4 \right[$
$g(x)=\frac{x\sqrt{16-{{x}^{2}}}}{2}\,,\,x\in \left] 0,4 \right[$
O perímetro e a área é máxima para $x=2\sqrt{2}\,cm$.
