Um paralelepípedo [ABCODEFG]
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 187 Ex. 54
Enunciado
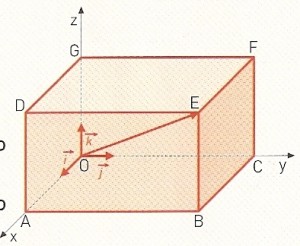No referencial o.n. $(O,\vec{i},\vec{j},\vec{k})$ da figura, está representado o paralelepípedo [ABCODEFG].
- $C\in \dot{O}y$ e $A\in \dot{O}x$
- $\overrightarrow{OE}=2\vec{i}+5\vec{j}+3\vec{k}$
- Indique as coordenadas dos vértices E, A e F.
- Defina, por uma condição, o plano perpendicular ao vetor dado que passa pelo ponto A.
- Determine, com aproximação às centésimas, a amplitude do ângulo que o vetor $\overrightarrow{OE}$ forma com o eixo Ox.
Resolução
As coordenadas desses pontos são: $E\,(2,5,3)$, $A\,(2,0,0)$ e $F\,(0,5,3)$.
- A equação desse plano é da forma $2x+5y+3z+d=0$.
Como A pertence a esse plano, as suas coordenadas têm de verificar a equação anterior. Logo, vem: $2\times 2+5\times 0+3\times 0+d=0\Leftrightarrow d=-4$.
Portanto, $2x+5y+3z-4=0$ é uma equação do plano considerado.
-
Ora, \[\cos (\overrightarrow{OE}\,\overset{\hat{\ }}{\mathop{{}}}\,\vec{i})=\frac{(2,5,3).(1,0,0)}{\sqrt{{{2}^{2}}+{{5}^{2}}+{{3}^{2}}}\times 1}=\frac{2}{\sqrt{38}}=\frac{2\sqrt{38}}{38}=\frac{\sqrt{38}}{19}\]
Logo, $\overrightarrow{OE}\,\overset{\hat{\ }}{\mathop{{}}}\,\vec{i}={{\cos }^{-1}}(\frac{\sqrt{38}}{19})\simeq 71,07{}^\text{o}$ é a amplitude pedida.
