Um ponto e um vetor
Geometria Analítica: Infinito 11 A - Parte 1 Pág. 176 Ex. 2
Enunciado
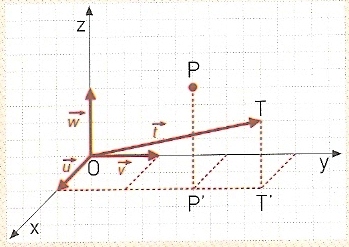Na figura está representado um referencial o. n. $(O,\vec{u},\vec{v},\vec{w})$, um ponto P e um vetor $\vec{t}\,(\vec{t}=\overrightarrow{OT})$.
Sendo P’ e T’ as projeções ortogonais de P e T no plano xOy,
- Indique as coordenadas de P e do vetor ${\vec{t}}$.
- Determine as coordenadas dos pontos Q, R e S, tais que: $Q=P+\vec{t}$, $R=P-2\vec{v}+\vec{t}$ e $S=P-2\vec{t}$.
Resolução
$P\,(1,2,\frac{3}{2})$.
Como $T\,(1,3,1)$, então $\vec{t}(1,3,1)$, pois $\vec{t}=\overrightarrow{OT}$.
- Ora,
\[\begin{array}{*{35}{l}}
Q & = & P+\vec{t} \\
{} & = & (1,2,\frac{3}{2})+(1,3,1) \\
{} & = & (2,5,\frac{5}{2}) \\
\end{array}\]
\[\begin{array}{*{35}{l}}
R & = & P-2\vec{v}+\vec{t} \\
{} & = & (1,2,\frac{3}{2})-2(0,1,0)+(1,3,1) \\
{} & = & (1,2,\frac{3}{2})-(0,2,0)+(1,3,1) \\
{} & = & (2,3,\frac{5}{2}) \\
\end{array}\]
\[\begin{array}{*{35}{l}}
S & = & P-2\vec{t} \\
{} & = & (1,2,\frac{3}{2})-2(1,3,1) \\
{} & = & (1,2,\frac{3}{2})-(2,6,2) \\
{} & = & (-1,-4,-\frac{1}{2}) \\
\end{array}\]
