Propriedades dos paralelogramos
Há quadriláteros que não têm lados paralelos (Não trapézios), outros que têm dois lados paralelos (Trapézios) e outros que têm os lados paralelos dois a dois. Estes últimos são os paralelogramos.
Paralelogramos são quadriláteros com dois pares de lados paralelos, isto é, têm os lados paralelos dois a dois.
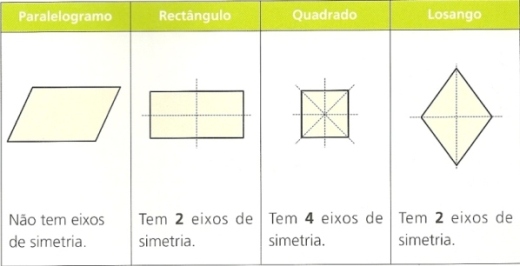
Pelas suas características particulares, no grupo dos quadriláteros paralelogramos podemos distinguir: o paralelogramo (propriamente dito), o retângulo, o losango e o quadrado. Explora a animação seguinte, de forma a recordares (ou descobrires) as diversas propriedades de cada um deles, relativamente aos ângulos, lados, diagonais e eixos de simetria:
Consideremos o paralelogramo [ABCD]:
Se considerarmos a diagonal [AC], o paralelogramo fica dividido em dois triângulos geometricamente iguais (ALA), porque:
- têm um lado comum: [AC];
- $B\hat{A}C=D\hat{C}A$ e $C\hat{A}D=A\hat{C}B$, pois são amplitudes de dois ângulos agudos (ou obtusos) de lados paralelos.
Logo, $\overline{AB}=\overline{DC}$ e $\overline{AD}=\overline{BC}$.
Os lados opostos de um paralelogramo têm o mesmo comprimento.
Por outro lado,
- $A\hat{B}C=A\hat{D}C$, porque são amplitudes de ângulos obtusos (ou agudos) de lados paralelos;
- $D\hat{A}B=D\hat{C}B$, porque são amplitudes de ângulos agudos (ou obtusos) de lados paralelos.
Os ângulos opostos de um paralelogramo têm a mesma amplitude.
Tracemos agora as diagonais [AC] e [DB]. Elas intersectam-se no ponto O.
Os triângulos [ABO] e [DCO] são geometricamente iguais (), pois
- $O\hat{A}B=D\hat{C}O$ e $A\hat{B}O=C\hat{D}O$, porque são as amplitudes de ângulos agudos (ou obtusos) de lados paralelos;
- $\overline{AB}=\overline{DC}$, pois [AB] e [DC] são lados opostos do paralelogramo.
Logo, $\overline{AO}=\overline{OC}$ e $\overline{DO}=\overline{OB}$.
As diagonais de um paralelogramo bissetam-se, isto é, dividem-se ao meio.
Podemos ainda provar (Como?) que
Dois ângulos consecutivos de um paralelogramo são suplementares.
Estuda os eixos de simetria nos quadriláteros paralelogramos:
