Mais assíntotas

\[\begin{array}{*{20}{l}}
{f\left( x \right) = \frac{{ – 2}}{{x – 2}}}&{}&{g\left( x \right) = \frac{{x – 7}}{{x + 2}}}&{}&{h\left( x \right) = \frac{{3x – 3}}{{2x + 4}}}
\end{array}\]

Função $f$

 Ora, \[f\left( x \right) = \frac{{ – 2}}{{x – 2}} = 0 – \frac{2}{{x – 2}}\]

Assíntota vertical:

\[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to {2^ – }} f\left( x \right) =  + \infty }&{\text{e}}&{\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) =  – \infty }
\end{array}\]

Logo, a reta de equação $x = 2$ é assíntota vertical bilateral do gráfico de $f$.

 Assíntota horizontal:

\[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to  – \infty } f\left( x \right) = {0^ + }}&{\text{e}}&{\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) = {0^ – }}
\end{array}\]

Logo, a reta de equação $y = 0$ é assíntota horizontal do gráfico de $f$, quando ${x \to  – \infty }$ e quando ${x \to  + \infty }$.

Função $g$

 Ora, \[g\left( x \right) = \frac{{x – 7}}{{x + 2}} = \frac{{x + 2 – 9}}{{x + 2}} = \frac{{x + 2}}{{x + 2}} + \frac{{ – 9}}{{x + 2}} = 1 – \frac{9}{{x + 2}}\]

Assíntota vertical:

 \[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to  – {2^ – }} g\left( x \right) =  + \infty }&{\text{e}}&{\mathop {\lim }\limits_{x \to  – {2^ + }} g\left( x \right) =  – \infty }
\end{array}\]

Logo, a reta de equação $x =  – 2$ é assíntota vertical bilateral do gráfico de $g$.

 Assíntota horizontal:

 \[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to  – \infty } g\left( x \right) = {1^ + }}&{\text{e}}&{\mathop {\lim }\limits_{x \to  + \infty } g\left( x \right) = {1^ – }}
\end{array}\]

Logo, a reta de equação $y = 1$ é assíntota horizontal do gráfico de $g$, quando ${x \to  – \infty }$ e quando ${x \to  + \infty }$.

Função $h$

 Ora, \[h\left( x \right) = \frac{{3x – 3}}{{2x + 4}} = \frac{{3\left( {x – 1} \right)}}{{2\left( {x + 2} \right)}} = \frac{{3\left( {x + 2 – 3} \right)}}{{2\left( {x + 2} \right)}} = \frac{3}{2}\left( {\frac{{x + 2}}{{x + 2}} + \frac{{ – 3}}{{x + 2}}} \right) = \frac{3}{2}\left( {1 – \frac{3}{{x + 2}}} \right) = \frac{3}{2} – \frac{{\frac{9}{2}}}{{x + 2}}\]

Assíntota vertical:

 \[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to  – {2^ – }} h\left( x \right) =  + \infty }&{\text{e}}&{\mathop {\lim }\limits_{x \to  – {2^ + }} h\left( x \right) =  – \infty }
\end{array}\]

Logo, a reta de equação $x =  – 2$ é assíntota vertical bilateral do gráfico de $h$.

 Assíntota horizontal:

 \[\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to  – \infty } h\left( x \right) = {{\tfrac{3}{2}}^ + }}&{\text{e}}&{\mathop {\lim }\limits_{x \to  + \infty } h\left( x \right) = {{\tfrac{3}{2}}^ – }}
\end{array}\]

Logo, a reta de equação $y = \frac{3}{2}$ é assíntota horizontal do gráfico de $h$, quando ${x \to  – \infty }$ e quando ${x \to  + \infty }$.

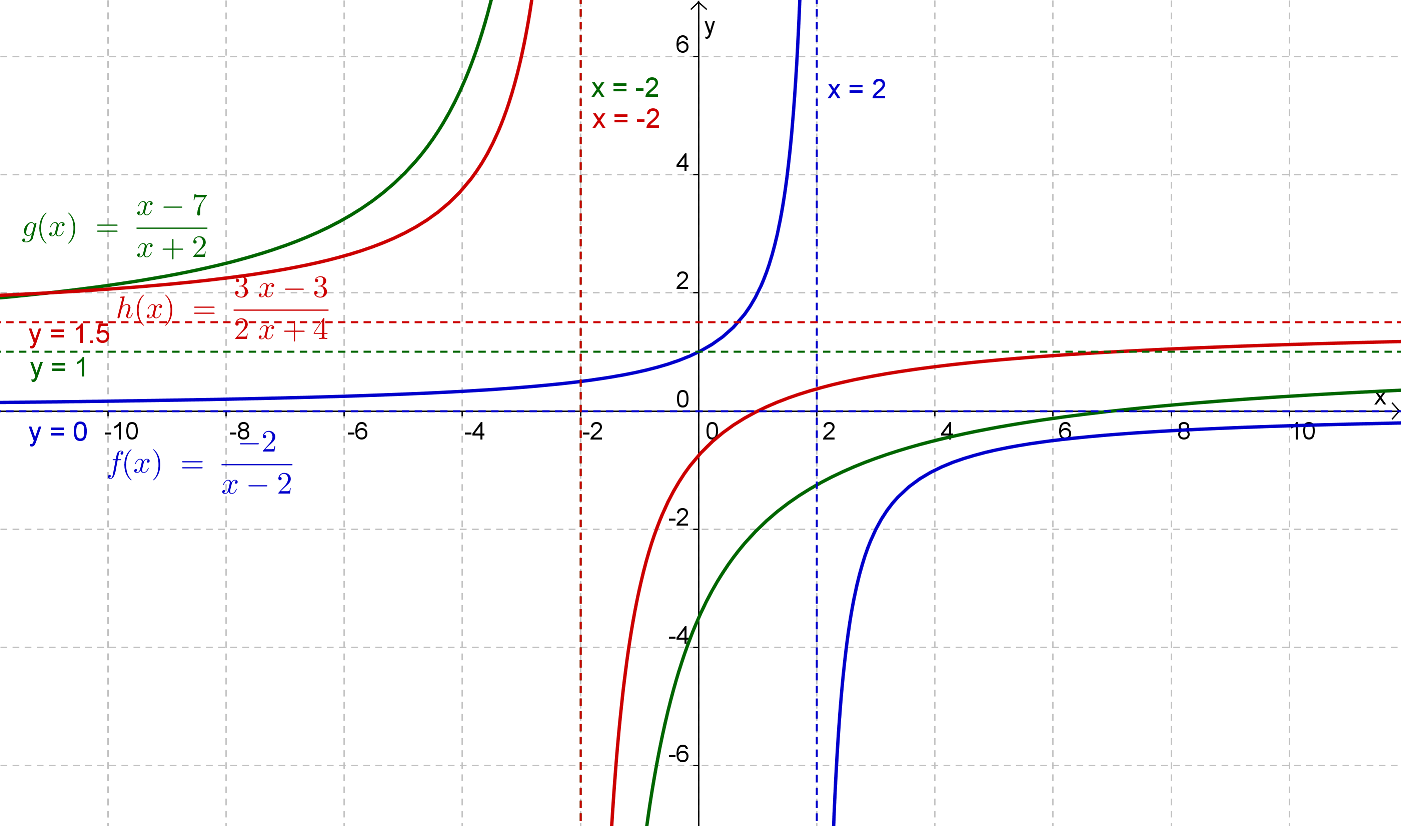
Apresenta-se de seguida os gráficos das três funções: