Um pentágono
Decomposição de figuras - Teorema de Pitágoras: Matematicamente Falando 8 - Parte 1 Pág. 33 Ex. 15
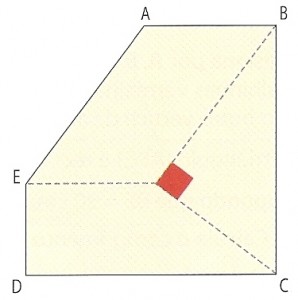O polígono [ABCDE] é a composição de um trapézio retângulo, um triângulo retângulo e um paralelogramo.
O cateto maior e a hipotenusa do triângulo retângulo medem, respetivamente, 80 cm e 100 cm.
A base maior do trapézio mede 102 cm e a menor 54 cm.
O ângulo BCD é reto.
Calcula:
- o perímetro do polígono [ABCDE];
- a área do polígono [ABCDE].
-
Aplicando o Teorema de Pitágoras no triângulo [BFC], temos:
$$\begin{array}{*{35}{l}}
{{\overline{FC}}^{2}}={{100}^{2}}-{{80}^{2}} & \Leftrightarrow & {{\overline{FC}}^{2}}=3600 \\
{} & \Leftrightarrow & \overline{FC}=\sqrt{3600} \\
{} & \Leftrightarrow & \overline{FC}=60 \\
\end{array}$$Aplicando o Teorema de Pitágoras no triângulo [CFG], temos:
$$\begin{array}{*{35}{l}}
{{\overline{FG}}^{2}}={{60}^{2}}-{{(102-54)}^{2}} & \Leftrightarrow & {{\overline{FG}}^{2}}=3600-2304 \\
{} & \Leftrightarrow & \overline{FG}=\sqrt{1296} \\
{} & \Leftrightarrow & \overline{FG}=36 \\
\end{array}$$O perímetro do polígono [ABCDE] é: \[\begin{array}{*{35}{l}}
P & = & \overline{AB}+\overline{BC}+\overline{CD}+\overline{DE}+\overline{EA} \\
{} & = & 54+100+102+36+80 \\
{} & = & 372\,cm \\
\end{array}\]
-
Calculando, sucessivamente, a área do triângulo, do trapézio e do paralelogramo, temos:
\[\begin{array}{*{35}{l}}
{{A}_{[BFC]}} & = & \frac{\overline{FB}\times \overline{FC}}{2} \\
{} & = & \frac{80\times 60}{2} \\
{} & = & 2400\,c{{m}^{2}} \\
\end{array}\]\[\begin{array}{*{35}{l}}
{{A}_{[CDEF]}} & = & \frac{\overline{CD}+\overline{EF}}{2}\times \overline{FG} \\
{} & = & \frac{102+54}{2}\times 36 \\
{} & = & 2808\,c{{m}^{2}} \\
\end{array}\]\[\begin{array}{*{35}{l}}
{{A}_{[ABFE]}} & = & \overline{AB}\times \overline{FH} \\
{} & = & 54\times (100-36) \\
{} & = & 3456\,c{{m}^{2}} \\
\end{array}\]Logo, o perímetro do polígono [ABCDE] é: \[A=2400+2808+3456=8664\,c{{m}^{2}}\]
