A altura da parede
Trigonometria: Matematicamente Falando 9 - Parte 2 Pág. 63 Ex. 17
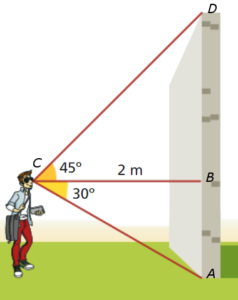O Gonçalo está a 2 m de uma parede, vê o seu topo segundo um ângulo de 45 graus e a sua base segundo um ângulo de 30 graus.
Determina a altura dessa parede.
Apresenta o resultado arredondado às décimas.
Nos triângulos retângulos [ABC] e [BCD], temos:
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} A\widehat CB = \frac{{\overline {AB} }}{{\overline {BC} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} 30^\circ = \frac{{\overline {AB} }}{2}}\\{}& \Leftrightarrow &{\frac{{\sqrt 3 }}{3} = \frac{{\overline {AB} }}{2}}\\{}& \Leftrightarrow &{\overline {AB} = \frac{{2\sqrt 3 }}{3}}\end{array}\]e
\[\begin{array}{*{20}{l}}{{\mathop{\rm tg}\nolimits} B\widehat CD = \frac{{\overline {BD} }}{{\overline {BC} }}}& \Leftrightarrow &{{\mathop{\rm tg}\nolimits} 45^\circ = \frac{{\overline {BD} }}{2}}\\{}& \Leftrightarrow &{1 = \frac{{\overline {BD} }}{2}}\\{}& \Leftrightarrow &{\overline {BD} = 2}\end{array}\]
A parede tem, aproximadamente, 3,2 metros de altura:
\[h = \overline {AB} + \overline {BD} = \frac{{2\sqrt 3 }}{3} + 2 \approx 3,2\]
