Hiparco e a distância à Lua
O incrível poder da matemática como uma ferramenta para modelar o nosso mundo
Resolução da Tarefa 1
Deduza a expressão \({\mathop{\rm crd}\nolimits} \alpha = 2{\mathop{\rm sen}\nolimits} \left( {\frac{\alpha }{2}} \right)\), tendo em consideração que \(\cos \left( {2\theta } \right) = {\cos ^2}\theta – {{\mathop{\rm sen}\nolimits} ^2}\theta \).
Seja \(r = 1\). Logo, \(A\left( {1,0} \right)\) e \(B\left( {\cos \alpha ,{\mathop{\rm sen}\nolimits} \alpha } \right)\).
Para todo o \(\alpha \in \left[ {0^\circ ,180^\circ } \right]\), aplicando o Teorema de Pitágoras no triângulo retângulo [ABB’] (B’ é a projeção ortogonal do ponto B sobre o eixo Ox) ou usando a fórmula da distância entre dois pontos, vem:
\[\begin{array}{*{20}{l}}{{\mathop{\rm crd}\nolimits} \alpha }& = &{\overline {AB} }\\{}& = &{\sqrt {{{\left( {1 – \cos \alpha } \right)}^2} + {{{\mathop{\rm sen}\nolimits} }^2}\alpha } }\\{}& = &{\sqrt {1 – 2\cos \alpha + {{\cos }^2}\alpha + {{{\mathop{\rm sen}\nolimits} }^2}\alpha } }\\{}& = &{\sqrt {2 – 2\cos \alpha } }\\{}& = &{\sqrt {2 – 2\cos \left( {2 \times \frac{\alpha }{2}} \right)} }\\{}& = &{\sqrt {2 – 2 \times \left( {{{\cos }^2}\left( {\frac{\alpha }{2}} \right) – {{{\mathop{\rm sen}\nolimits} }^2}\left( {\frac{\alpha }{2}} \right)} \right)} }\\{}& = &{\sqrt {2 – 2 \times \left( {1 – {{{\mathop{\rm sen}\nolimits} }^2}\left( {\frac{\alpha }{2}} \right) – {{{\mathop{\rm sen}\nolimits} }^2}\left( {\frac{\alpha }{2}} \right)} \right)} }\\{}& = &{\sqrt {4 \times {{{\mathop{\rm sen}\nolimits} }^2}\left( {\frac{\alpha }{2}} \right)} }\\{}& = &{2 \times {\mathop{\rm sen}\nolimits} \left( {\frac{\alpha }{2}} \right)}\end{array}\]
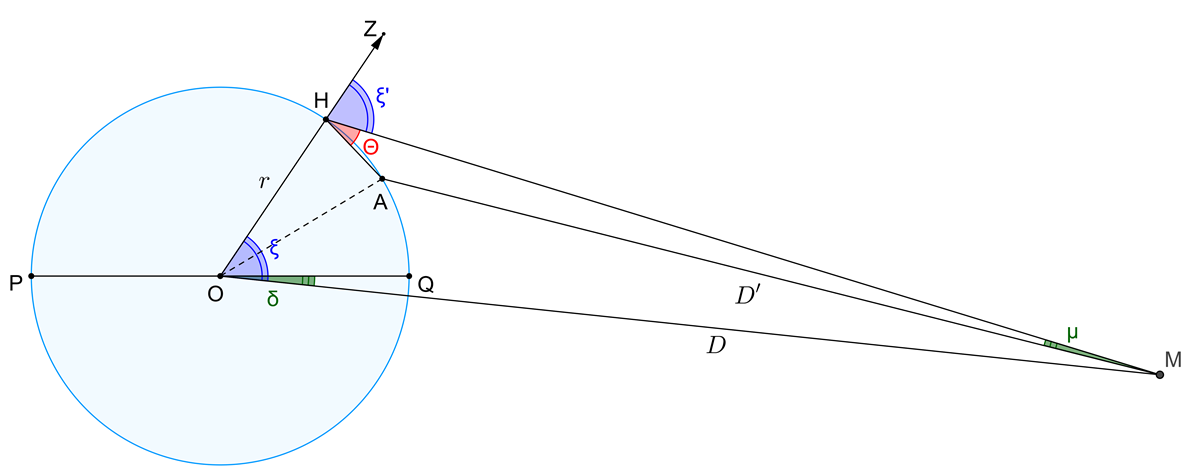
Resolução da Tarefa 3
Tenha em consideração as seguintes aproximações:
- \(\zeta ‘ \approx \zeta \)
- \(D = D’ + r\)
Dados conhecidos:
- Latitude de Helesponto: \({\phi _H} = 41^\circ \)
- Latitude de Alexandria: \({\phi _A} = 31^\circ \)
- Declinação da Lua: \(\delta = – 3^\circ \)
- Paralaxe lunar: \(\mu = 0,1^\circ \)
A distância zenital da lua em H, \(\zeta ‘\), é aproximadamente igual a \(\zeta \), sendo \(\zeta = {\phi _H} – \delta = 41^\circ + 3^\circ = 44^\circ \).
No triângulo isósceles [AOH], sabe-se que \(A\widehat OH = {\phi _H} – {\phi _A} = 10^\circ \). Logo, \(A\widehat HO = H\widehat AO = \frac{{180^\circ – 10^\circ }}{2} = 85^\circ \).
Assim, \(\theta = 180^\circ – \zeta ‘ – O\widehat HA \approx 180^\circ – 44^\circ – 85^\circ \approx 51^\circ \).
O comprimento da corda [AH], em função de $r$, pode ser expresso por:
\[\overline {AH} = r \times {\mathop{\rm crd}\nolimits} \left( {A\widehat OH} \right) = r \times {\mathop{\rm crd}\nolimits} \left( {{\phi _H} – {\phi _A}} \right) = 2r \times {\mathop{\rm sen}\nolimits} \left( {\frac{{{\phi _H} – {\phi _A}}}{2}} \right)\]
Por aplicação da lei dos senos no triângulo [AHM], temos:
\[\begin{array}{*{20}{c}}{\frac{{\overline {AH} }}{{{\mathop{\rm sen}\nolimits} \mu }} = \frac{{D’}}{{{\mathop{\rm sen}\nolimits} \theta }}}& \Leftrightarrow &{D’ = \overline {AH} \times \frac{{{\mathop{\rm sen}\nolimits} \theta }}{{{\mathop{\rm sen}\nolimits} \mu }}}\end{array}\]
Pelas duas relações anteriores, vem:
\[D’ = 2r \times {\mathop{\rm sen}\nolimits} \left( {\frac{{{\phi _H} – {\phi _A}}}{2}} \right) \times \frac{{{\mathop{\rm sen}\nolimits} \theta }}{{{\mathop{\rm sen}\nolimits} \mu }}\]
Substituindo os valores conhecidos na fórmula anterior, temos:
\[D’ = 2r \times {\mathop{\rm sen}\nolimits} \left( {\frac{{41^\circ – 31^\circ }}{2}} \right) \times \frac{{{\mathop{\rm sen}\nolimits} 51^\circ }}{{{\mathop{\rm sen}\nolimits} 0,1^\circ }} \approx 77,6 \times r \approx 78 \times r\]
Este valor está substancialmente afastado do referido no texto.
Considerando, agora, um valor mais preciso da paralaxe lunar (\(\mu = \frac{1}{5} \times \frac{{360 \times 60′}}{{650}} \approx 6,65′ \approx 0,11^\circ \)) referido no texto de G. J. Toomer, temos:
\[D’ = 2r \times {\mathop{\rm sen}\nolimits} \left( {\frac{{41^\circ – 31^\circ }}{2}} \right) \times \frac{{{\mathop{\rm sen}\nolimits} 51^\circ }}{{{\mathop{\rm sen}\nolimits} 0,11^\circ }} \approx 70,56 \times r \approx 71 \times r\]
Este valor está mais próximo do indicado em ambos os textos, resultando, neste caso, \(D \approx D’ + r \approx 72 \times r\).