A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Tagged: reflexão axial

0

Aplicando / 8.º Ano / Isometrias

Observa as figuras

Isometrias: Matematicamente Falando 8 - Pág. 113 Ex. 5

Enunciado

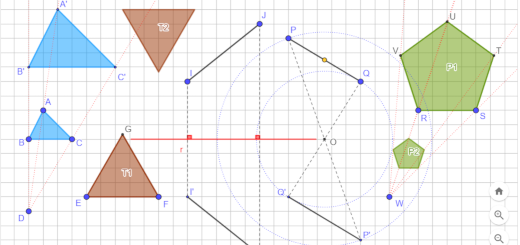
Observa as figuras.

As figuras F1 e F2 são imagens da figura F obtidas por meio das seguintes isometrias:
[A] Reflexão axial seguida de rotação;
[B] Reflexão deslizante seguida de rotação;
[C] Translação seguida de rotação;
[D] Rotação seguida de meia-volta.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Isometrias

Identifica a isometria

Isometrias: Matematicamente Falando 8 - Pág. 110 Ex. 15

Enunciado

Copia, para uma folha de papel quadriculado, o seguinte pentágono.

  1. Desenha o transformado do pentágono por reflexão de eixo m1 e a imagem deste pela reflexão de eixo m2.
  2. Identifica uma isometria que transforme o primeiro no último pentágono.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Isometrias

Identifica a isometria

Isometrias: Matematicamente Falando 8 - Pág. 110 Ex. 14

Enunciado

Copia, numa folha de papel quadriculado, o hexágono.

Desenha a reflexão desse hexágono em relação ao eixo e1 e depois faz a reflexão do segundo hexágono que desenhaste em relação ao eixo e2.

Identifica uma isometria que transforma o primeiro hexágono no terceiro.

Resolução >> Resolução

<< Enunciado… Ler mais
0

8.º Ano / Isometrias / Aplicando

Quatro frisos

Isometrias: Matematicamente Falando 8 - Pág. 105 Tarefa 11 Ex. 2

Enunciado

Usando blocos, o Joel construiu os seguintes frisos e representou-os no caderno.

Indica que isometrias deixam cada friso invariante, ou seja, o transforma nele próprio.
Copia e completa a tabela e regista as tuas conclusões.

Translação Reflexão axial Rotação Reflexão deslizante
Eixo vertical Eixo horizontal
Sim/Não Sim/Não Sim/Não Sim/Não Sim/Não
Friso 1          
…          

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Isometrias

A nova estrada

Isometrias: Matematicamente Falando 8 - Pág. 103 Ex. 10

Enunciado

Na figura, podemos ver a nova estrada que foi construída perto das vilas de Cima e de Baixo.

Nessa estrada, será feita uma abertura de onde sairão os caminhos, um para cada uma das vilas.

Determina o ponto da estrada onde deverá ser feita essa abertura, de forma a garantir que o trajeto entre as duas vilas é o mais curto possível.

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Isometrias

Quais das seguintes afirmações são falsas?

Isometrias: Matematicamente Falando 8 - Pág. 103 Ex. 9

Enunciado

Quais das seguintes afirmações são falsas?
Nesses casos, apresenta um contra exemplo.

  1. Toda a semelhança é uma isometria.
  2. Se dois triângulos equiláteros são iguais, então um é sempre o transformado do outro por uma translação.
  3. Numa reflexão axial, um segmento de reta é sempre transformado num segmento de reta paralelo.
  4. Numa meia-volta, um segmento de reta é sempre transformado num segmento de reta paralelo.
  5. Se dois pentágonos são semelhantes, então um é sempre a imagem do outro
… Ler mais
0

Aplicando / 8.º Ano / Isometrias

Na aula de Matemática

Isometrias: Matematicamente Falando 8 - Pág. 103 Ex. 8

Enunciado

Na aula de Matemática, a professora propôs que os alunos escolhessem uma translação, uma rotação de centro num ponto da figura ou uma reflexão cujo eixo intersetasse a figura e construíssem o transformado da figura acima.

A Catarina perguntou ao Ismael que isometria iria escolher, ao que ele lhe  respondeu: “Apenas te digo que nenhum ponto ficará fixo.”

Será esta resposta suficiente para saber qual é a isometria escolhida pelo Ismael?
Explica a tua resposta.

Resolução >>… Ler mais

0

Aplicando / 8.º Ano / Isometrias

Observa as figuras

Isometrias: Matematicamente Falando 8 - Pág. 102 Ex. 3

Enunciado

Observa as figuras.

  1. Existe uma única figura onde as duas imagens podem ser relacionadas por meio de uma translação. Identifica-a.
  2. Quais são as figuras em que uma imagem é obtida da outra através de uma reflexão axial?
  3. Qual é a figura em que uma imagem é obtida da outra através de uma meia-volta?
  4. Qual é a figura em que uma imagem é obtida da outra através de uma reflexão deslizante?

Resolução >> Resolução

<< Enunciado… Ler mais
0

Aplicando / 8.º Ano / Isometrias

Os triângulos são todos iguais e equiláteros

Isometrias: Matematicamente Falando 8 - Pág. 102 Ex. 2

Enunciado

Na figura, os triângulos numerados são todos iguais e equiláteros.

  1. Caracteriza:
    a) uma rotação, uma translação e uma reflexão axial que transformem o triângulo 4 no triângulo 6;
    b) duas isometrias diferentes que transformem o triângulo 9 no triângulo 8.
  2. Relaciona com \({\vec u}\) e \({\vec v}\) o vetor da translação que transforma:
    a) o triângulo 9 no triângulo 18;
    b) o triângulo 3 no triângulo 16;
    c) o triângulo 16 no triângulo 1.

Resolução >> Resolução… Ler mais