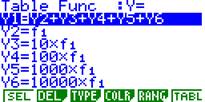Escola Secundária/3 da Sé-Lamego

Ficha de Trabalho de Matemática

 

Ficha de Trabalho com Proposta de Resolução em formato PDF

1.   O TOTOLOTO 6/49
O Totoloto surgiu em 1985. Criado pelo Decreto-Lei n.º 382/82 de 15 de Setembro só mais tarde, através do Decreto-Lei n.º 84/85, de 28 de Março, o Estado concedeu à SCML o direito à sua organização e exploração.
O primeiro concurso realizou-se a 30 de Março desse ano.
O jogo consiste na escolha de seis números, entre 49 possibilidades.
Assim, os prognósticos são efectuados traçando as cruzes nos quadradinhos e estabelecendo conjuntos de seis números.
Os prémios são atribuídos a partir do acerto em três dos números escolhidos.
As apostas simples têm de ser em número par (2, 4, 6, 8 e 10 apostas), começando pelos dois primeiros conjuntos da esquerda e continuando sem intervalo.
Em cada conjunto, marcam-se com cruzes (X), os seis números escolhidos.
As apostas múltiplas fazem-se sempre no conjunto 1 dos bilhetes. Podem ser preenchidas 7 a 12 números, assinalando o quadradinho referente às apostas mútuas.
No início de 1988 surgiu uma nova modalidade de aposta de aposta múltipla, o 5/44. O apostador escolhe 5 números fixos que combinam uma vez, com cada um dos restantes 44, perfazendo um total de 44 apostas.
O bilhete de cinco semanas permite participar em cinco concursos seguidos, com os mesmos conjuntos de números.
http://www.djogos.scml.pt/totoloto/historia/index.html

 

Ampliar

 

 

Nota: O preço unitário da aposta é € 0,35 para o Totoloto e de € 0,75 para o Joker.

 

a)   Justifique que a aposta múltipla de 11 cruzes corresponde a 462 apostas simples.

b)   Por que razão a aposta múltipla de 5 cruzes custa € 15,40 ?

c)   Para 12 cruzes marcadas e apenas em relação aos casos de 3 e 4 acertos, explicando o seu raciocínio, comprove os valores indicados.

Proposta de resolução

2.   Um Jogo de 5 Dados

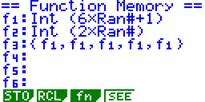
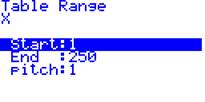
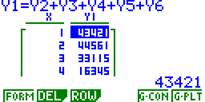
      Lançam-se cinco dados.
Para ganharmos tem de sair o número 5 mas não pode sair o 6.
Qual é a probabilidade de ganhar?

a)   Efectuando uma simulação com a calculadora gráfica obtenha experimentalmente uma aproximação razoável para essa probabilidade.

             Sugestão:

      Certamente ainda tem definida na sua calculadora CASIO a função  que permite simular o lançamento de um dado. Defina as 6 funções conforme aparece na imagem em baixo, defina a RANG sugerida e obtenha a tabela com os 250 valores de .

                        

 

 

                       

 

             Nota: No exemplo, nas 4 primeiras jogadas feitas, só ganhámos na terceira.

Faça a contagem das vitórias obtidas nessas 250 jogadas. De seguida junte os seus resultados aos dos restantes colegas da turma.

b)   Determine o valor teórico dessa probabilidade.
Faça um comentário sobre os dois valores determinados.

Proposta de resolução

3.   Três Bilhetes de Cinema

      Resolva por quatro processos o seguinte problema:

      A professora de História resolveu levar os seus 15 alunos a ver um filme.
Como o cinema tem filas de precisamente 15 cadeiras, comprou uma fila inteira e distribuiu os bilhetes ao acaso pelos alunos.
A Ana, a Bela e a Carla são muito amigas e gostavam de ficar as três juntas e numa das pontas da fila.

      Qual é a probabilidade de isso acontecer?

Proposta de resolução

 

«Uma questão que se coloca muitas vezes perante os problemas de Probabilidades é o facto de existirem vários processos de os resolver. Normalmente isso sucede por, perante a situação descrita no problema, se poderem considerar diferentes espaços de resultados conforme a abordagem que se faça. Para calcular a probabilidade aplicando a definição de Laplace, devemos dividir o número de casos favoráveis pelo número de casos possíveis. Ora, a cada espaço de resultados irá corresponder um diferente número de casos possíveis e, claro, um diferente número de casos favoráveis.

O principal cuidado a ter é usar exactamente o mesmo método na contagem dos casos favoráveis e na contagem dos casos possíveis, ou seja, não mudar de espaço de resultados a meio da resolução.»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Proposta de Resolução:

1.   O TOTOLOTO 6/49

a)   A aposta simples é constituída pela selecção de 6 dos 49 números, de 1 a 49.
Ao efectuar uma aposta múltipla de 11 cruzes estamos a seleccionar 11 desses 49 números.
Ao convertermos essa aposta múltipla em apostas simples temos de seleccionar de cada vez apenas 6 desses 11 números. Cada uma dessas apostas diferirá das outras quando pelo menos um dos números seleccionados é diferente, não interessando a ordem por que são escolhidos. Trata‑se, portanto, de determinar quantos subconjuntos de 6 elementos é possível obter de um conjunto de 11.
Assim, a aposta múltipla de 11 cruzes corresponde a  apostas simples.

b)   A chave do Totoloto é constituída por 6 números. O apostador ao marcar 5 cruzes não selecciona 44 dos 49 números. Cada um destes números é, por sua vez, integrado automaticamente no grupo dos 5 marcados.
Desta forma, a aposta múltipla de 5 cruzes corresponde a 44 apostas simples. Daí que o seu preço seja de  €  € .

c)   Para 3 acertos:

Das 12 cruzes, três delas assinalam 3 números certos (C) - pertencentes à chave - e as restantes nove assinalam 9 números errados (E) - não pertencentes à chave.

C C C E E E E E E E E E

Como a aposta simples é composta por 6 cruzes (seis números), convertendo a aposta múltipla em apostas simples conclui‑se que as apostas premiadas, além das três cruzes certas, serão completadas com 3 cruzes erradas.

Assim, o número de apostas (simples) premiadas com o 5.º prémio (3 números certos) será .

Para 4 acertos:

Raciocinando da mesma maneira, temos agora a situação: C C C C E E E E E E E E
Para o 4.º prémio será: .
Para o 5.º prémio será: .(Note que para este prémio apenas há 3 números certos em cada uma das apostas simples premiadas com o 5.º prémio, ficando, portanto, um deles de fora)

 

2.   Um Jogo de 5 Dados

a)   Efectuada uma simulação com a calculadora gráfica foram obtidos os seguintes resultados:
N.º de lançamentos: 250
N.º de vitórias: 69
O valor experimental obtido é .

b)   Um processo:

O número de casos possíveis quando são lançados cinco dados são os arranjos com repetição dos 6 números: .

O número de casos favoráveis (sair 5 mas não sair 6) tem de ser feito em duas etapas.

Primeiro, não pode sair 6: são os arranjos com repetição dos números de 1 a 5.
                Casos em que não sai 6 : .

Segundo, não pode sair 6 mas tem de sair 5. Então, aos 3125 casos anteriores temos de subtrair os casos em que também não sai 5.
                Casos em que não sai 6 nem 5: .

      Casos em que não sai 6 mas sai 5: .
Logo, .
A probabilidade de ganhar o jogo é praticamente igual a 27%.

Outro processo:

      Podemos decompor os lançamentos favoráveis em cinco tipos:

·       sair cinco "5" e zero "6":      

·       sair quatro "5" e zero "6":    

·       sair três "5" e zero "6":         

·       sair dois "5" e zero "6":        

·       sair um "5" e zero "6":          

(As combinações são relativas ao número de maneiras de sair exactamente o número de "5" e os arranjos com repetição relativos ao número de maneiras de não sair "6" nem "5", isto é, de sair "1", "2", "3" ou "4".)

Logo, .

 

3.   Três Bilhetes de Cinema

 

      1.º Processo

      Vamos pensar apenas nos três bilhetes destinados às três amigas, não nos interessando a ordem como elas ocuparão depois esses três lugares.

      O espaço de resultados é o conjunto dos ternos não ordenados. Por exemplo, um dos seus elementos é o terno , que corresponde às três amigas receberem os bilhetes 5, 7 e 15 embora não saibamos o lugar exacto em que cada uma delas se vai sentar.

      Os casos possíveis são as diferentes maneiras de elas receberem os 3 bilhetes de um conjunto de 15, ou seja, todos os ternos não ordenados formados a partir do conjunto de 15 bilhetes.

      Casos Possíveis: .

      Os casos favoráveis são apenas 2: ou recebem os bilhetes 1-2-3 ou os bilhetes 13-14-15.

      Logo, .

 

      2.º Processo

      Vamos pensar nos três bilhetes destinados às três amigas, mas interessando-nos agora a ordem como elas ocuparão depois esses três lugares. Continuamos a ignorar os outros 12 bilhetes.

      O espaço de resultados é o conjunto dos ternos ordenados. Por exemplo, um dos seus elementos é o terno , ou seja, a Ana fica no lugar 5, a Bela no 7 e a Carla no 15.

      Os casos possíveis são portanto as diferentes maneiras de elas receberem 3 bilhetes de um conjunto de 15, mas em que a ordem por que recebem os bilhetes é importante.

      Casos Possíveis: .

      Se os bilhetes que elas receberem forem 1, 2 e 3, como a ordem interessa, há seis maneiras de elas os ocuparem (são as permutações de 3). O mesmo se passa para os bilhetes 13, 14 e 15.

      Logo, os casos favoráveis são: .

      Assim, .

 

      3.º Processo

      Desta vez vamos considerar todas as maneiras como os 15 alunos se podem sentar nos 15 lugares.

      O espaço de resultados é constituído por todas as permutações dos 15 alunos pelas cadeiras.

      Os casos possíveis são portanto as permutações de 15.

      Casos Possíveis: .

      Se as três amigas ficarem nos lugares 1, 2 e 3, podem permutar entre si, e os outros 12 alunos também. O mesmo se passa se ficarem nos três últimos lugares. Então:

      Casos Favoráveis: .

      Logo, .

 

      4.º Processo

      Vamos calcular a probabilidade pedida admitindo que os bilhetes vão ser entregues um a um às três amigas.

      A primeira vai receber o seu bilhete. Dos 15 lugares, há 6 que lhe servem (os três primeiros e os três últimos).

      Chegou a vez da segunda. Há 14 bilhetes e a ela só servem os dois lugares que restam na ponta onde a primeira ficou.

      Finalmente, a terceira, dos 13 bilhetes restantes, tem de receber o único que sobra na ponta onde estão as amigas.

      Logo, .

 

 

 

 

Portanto, NÃO ESQUEÇA: