Ficha de Trabalho de Matemática
Trabalho
de Grupo
Ano Lectivo 2004/05 Ângulos internos de um triângulo 7.º
Ano
1.ª Parte
Manuseando triângulos
A. Constrói um qualquer triângulo em cartolina.
(Observa as figuras apresentadas abaixo)
Pinta parte dos seus ângulos internos, junto a cada um dos vértices, e
numera-os.
Corta o triângulo em três pedaços, de forma semelhante à apresentada:
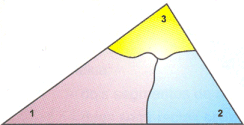
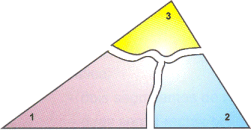
Utilizando os
três pedaços, tenta fazer um ângulo constituído por 1, 2 e 3.
É possível?
Se sim, que ângulo obténs?
B. Constrói um
qualquer triângulo em papel ou papel de lustro.
Dobra o triângulo que construíste como é indicado na figura seguinte. Isto é,
fazendo com que o vértice oposto fique sobre o lado maior do triângulo e que a
dobra fique paralela a esse lado.
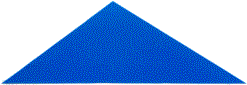

Agora faz
mais duas dobras, perpendiculares à base do triângulo, de forma que os
restantes dois vértices fiquem encostados ao primeiro vértice. (Em caso de
dúvida, observa na animação os procedimentos a efectuar.)
O que é que
verificas? Porque será?
O que aconteceu com os teus colegas dos outros grupos? Dependerá do triângulo
considerado?
O resultado
obtido pode também ser conseguido recorrendo a duas transformação geométricas.
Uma delas é já tua conhecida. Executa os procedimentos indicados na animação
apresentada seguidamente e identifica a transformação geométrica já tua
conhecida e descreve a outra.
2.ª Parte
Um programa de geometria dinâmica: Cinderella
C. Agora vais
ver como se pode investigar esta mesma propriedade dos triângulos com o
programa de geometria dinâmica Cinderella.
|
1. Começa por
construir um triângulo [ABC].
|
|
· cria três pontos (chama-lhes A, B
e C);
|
|
· constrói os três lados do
triângulo (são os segmentos que unem os pontos dois a dois);
|
|
· arrasta um dos vértices do
triângulo e verifica que o triângulo muda de forma mas não se desfaz.
|
|
2.
Pede ao Cinderella que meça as amplitudes dos ângulos
internos do triângulo [ABC].
|
|
3.
Arrasta um vértice qualquer do triângulo e verifica que os
valores dos ângulos variam.
|
Continuas a
obter a relação obtida na 1.ª Parte?
Enuncia a propriedade que verificas relativamente aos ângulos internos de um
triângulo.
Se já
conheces o programa Cinderella, podes usá-lo para fazer a construção
acima descrita.
Em caso negativo, resolve este exercício:
3.ª Parte
Um pouco de História
D. A propriedade que enunciaste na questão
anterior, «A soma das amplitudes dos ângulos internos de um triângulo é 180º.»,
é, certamente, já do teu conhecimento e já a aplicaste algumas vezes.
Mas, será
verdadeira essa afirmação?
Não poderá acontecer que o resultado obtido nas experiências anteriores seja um
valor próximo de 180º, sem ser exactamente 180º?
Confessa que
agora ficaste confuso... Mas, então é ou não é igual a 180º?
Julga-se que Tales (624 – 547
a. C.)
terá usado o facto de que a soma dos ângulos de um triângulo é igual a dois
rectos. No entanto não há provas que tenha demonstrado essa afirmação.
É considerado certo que os matemáticos da escola de Pitágoras (cerca de
580 – 500 a. C. ) teriam demonstrado o teorema "todo o triângulo tem os
ângulos internos iguais a dois ângulos rectos", com base numa axiomática
(conjunto de noções admitidas sem demonstração, que formam um ramo cujo
conteúdo se deduz pelo raciocínio) considerada rudimentar nos dias de hoje e,
na época, considerada insatisfatória por Aristóteles (384 – 322
a. C.).

ver linha do tempo
Cerca do séc. III a. C., após a criação da obra Os Elementos por
Euclides
(cerca de 325 – 265 a. C.), a incapacidade demonstrativa da relação entre os
ângulos formados por uma transversal incidindo em duas paralelas, quer a
igualdade a dois rectos dos ângulos internos dum triângulo ficou resolvida.
Euclides, para validar toda a sua obra de geometria, dita Euclideana, formulou
uma afirmação que (por princípio) se aceita como verdadeira para o
desenvolvimento dessa teoria geométrica, e que pode ser enunciada da seguinte
forma:
Se uma linha
recta incidir em duas linhas rectas e fizer os ângulos internos do mesmo lado
menores do que dois ângulos rectos, as duas linhas rectas, se prolongadas
indefinidamente, encontram-se do lado em que os ângulos são menores do que dois
ângulos rectos.

Nota: Um postulado é uma afirmação cuja veracidade
se aceita sem prova.
|
Explora a animação
seguinte, para perceber melhor esta afirmação de Euclides, que é conhecida por
o 5.º Postulado de Euclides.
No século XVIII, o matemático britânico John
Playfair apresentou uma formulação equivalente ao 5.º postulado, mas mais
simples do que a frase de Euclides:
Dada uma recta
e dado um ponto exterior a ela, existe uma e uma só recta paralela à recta dada
e passando pelo ponto dado.
|
4.ª Parte
A igualdade de ângulos alternos internos
E. Completa a demonstração do seguinte teorema:
|
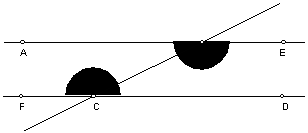
Hipótese: As rectas AB e
CD são paralelas e a recta BC é uma sua transversal.
|
|
Tese: Os
ângulos ABC e BCD são iguais.
|
|
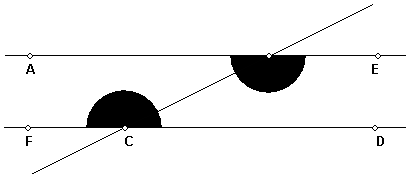
|
|
Demonstração:
|
|
|
|
Caso 1: o ângulo ABC é menor que o ângulo BCD.
|
|
Nesta circunstância, a soma dos
ângulos ABC e BCF é __________ a dois rectos, pelo que, de acordo com o
postulado 5.º, as rectas AB e CD se _______________ do lado destes ângulos. O
que é absurdo, pois por construção as rectas AB e CD são ___________. Logo,
não é verdade que o ângulo ABC é
__________ que o ângulo BCD.
|
|
|
|
|
|
Caso 2: o ângulo ABC é maior que o ângulo BCD.
|
|
Nesta circunstância, a soma dos
ângulos BCD e CBE é __________ a dois rectos, pelo que, de acordo com o
postulado 5. , as rectas AB e CD se _______________ do lado destes
ângulos. O que também é absurdo, pois por construção as rectas AB e CD são
___________. Logo, também não é verdade que o ângulo ABC é __________ que o ângulo BCD.
|
|
|
|
Conclusão: Portanto, não sendo diferentes,
os ângulos ABC e BCD são iguais.
|
5.ª Parte
A demonstração
F. Para as duas
situações apresentadas a seguir, usando o resultado demonstrado anteriormente,
prova que:
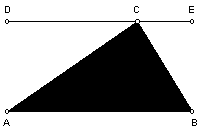
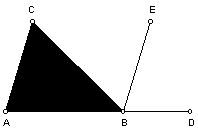
Num triângulo, a soma das
amplitudes dos seus ângulos internos é 180º.
|
|
|
|
As rectas AB e DC são paralelas
|
As rectas AC e BE são paralelas
|
6.ª Parte
Para evitar surpresas... e alguns extras
G. Para evitar
surpresas num futuro próximo, deixo-te aqui uma ligação:
http://www.geocities.com/thesciencefiles/anglesum/page.html
(Página traduzida para
português)
Surpreendido?
Se estás curioso e queres saber alguma coisa sobre estas novas geometrias,
sugiro-te a leitura seguinte:
Ao longo da história, o 5.º postulado causou alguma
estranheza e desconforto. A complexidade da frase, por comparação com a
simplicidade das frases que exprimem os 4 primeiros postulados, convenceu
alguns geómetras de que o 5.º
postulado poderia talvez ser demonstrado (e, portanto, deixaria de
ser "postulado" e passaria a ser "proposição"). Esta
convicção originou muitas pesquisas que só terminaram no séc. XIX, quando Lobatschewski
e Bolyai
conceberam geometrias que satisfazem os 4 primeiros postulados e não satisfazem
o 5.º. Isso veio mostrar que o 5.º postulado não pode ser uma consequência dos
outros 4; portanto Euclides tinha razão: trata-se mesmo dum postulado!
Nas geometrias concebidas por Lobatschewski e por Bolyai, o
5.º postulado de Euclides não se verifica; geometrias assim dizem-se "não-euclidianas".
Carlos Sá
Pergunte Agora
|
Os 4
primeiros postulados de Euclides são:
1.
Dados dois pontos, pode traçar-se uma recta que
passa por ambos;
2.
Pode prolongar-se uma linha recta dada;
3.
Dados dois pontos, pode traçar-se uma
circunferência com centro num deles e que passe pelo outro;
4.
Todos os ângulos rectos são iguais.
H. Podes
encontrar o enunciado do 5.º Postulado numa edição portuguesa de 1855 dos Elementos
de Euclides, no seguinte endereço:
http://www.mat.uc.pt/~jaimecs/euclid/2parte.html
Nesta versão,
o 5.º Postulado corresponde ao Axioma XII.
I. A
demonstração que efectuámos na 5.ª parte também foi feita por Euclides nos Elementos.
Podes apreciar essa prova estudando a Prop. XXXII, neste endereço:
http://www.mat.uc.pt/~jaimecs/euclid/4parte.html
Podes
apreciar também essa demonstração na seguinte animação:
Se
pretenderes perceber ou conhecer as justificações indicadas entre parêntesis na animação
anterior, podes consultá-las em português no endereço seguinte:
http://www.prof2000.pt/users/zemaria/CINDERELLA/Tarefa_5_P32.htm
Nota: A diferença que
notas entre a terminologia usada para referenciar as diversas justificações é
devido a, em cada um dos casos, se ter usado versões diferentes dos Elementos
de Euclides.
FIM
Página
actualizada em 05-12-2004









