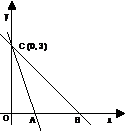Escola Secundária/3 da Sé-Lamego

Ficha de Trabalho de Matemática

 

Nos exercícios 1 e 2 explora o sketch GSP em:

http://www.prof2000.pt/users/amma/recursos_materiais/rec/10_ano/f_trab/2002_03/funcao_afim.gsp

http://www.prof2000.pt/users/amma/recursos_materiais/rec/10_ano/f_trab/2002_03/f_afim.htm

Nota:  Podes utilizar ainda o programa Graphmatica ou a calculadora gráfica.

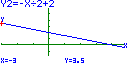
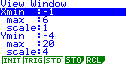
1.   Os gráficos das funções (de domínio  ) do tipo  são rectas.
Nestas funções, m e b têm um significado especial.

a)   Observa o gráfico de algumas delas, fixando um valor para b e atribuindo a m os valores concretos que entenderes - positivos, negativos,... Que verificas?

b)   Qual a influência do parâmetro m nos gráficos desta família de funções?

c)   Estuda ainda a família de funções , fixando agora um valor para m e atribuindo a b os valores que entenderes. Que verificas?

d)   Qual a influência do parâmetro b nos gráficos desta família de funções?

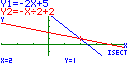
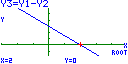
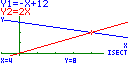
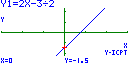
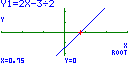
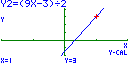
2.   Faz uma síntese, oral, do estudo da função afim: .
Refere-te ao tipo de gráfico, domínio, contradomínio, monotonia, zeros, intersecção com os eixos, sinal da função, coordenadas de um vector director da recta que define o seu gráfico.

3.   Escreve a expressão analítica e representa graficamente a função afim cujo gráfico é uma recta que:

a)   tem declive 2 e ordenada na origem 5;

b)   tem declive  e contém o ponto de coordenadas (0, 2).

Solução

4.   Relativamente às funções da questão anterior, resolve as questões seguintes e depois confirma os resultados graficamente.

a)   Resolve analiticamente a equação .

b)   Resolve analiticamente a inequação .

Solução (Nota: A resolução apresentada em b) não é a correspondente ao pedido)

5.   A média de dois números x e y é 6.

a)   Escreve uma equação que traduza a condição e resolve-a em ordem a y.

b)   Indica três pares de números nas condições referidas.

c)   Se um dos números é dobro do outro, quais são os números?
Resolve o problema algébrica e geometricamente.

Solução

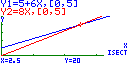
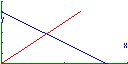
6.   Observa a figura seguinte e, de acordo com os dados, determina a expressão analítica da função afim cujo gráfico é a recta:

a)   AC, sabendo que a área do triângulo [OAC] é .

b)   BC, sabendo que o triângulo [OBC] é isósceles.

Nota:  Para verificares a tua resposta, utiliza o seguinte sketch GSP:
http://www.prof2000.pt/users/amma/recursos_materiais/alabmat/0_ficheiros/Eq_recta.gsp

Solução

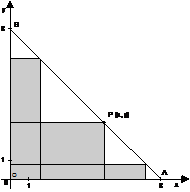
7.   No referencial está representado um triângulo rectângulo isósceles [OAB].
O ponto P pertence ao segmento [AB] e é um dos vértices de um rectângulo cujos lados são paralelos aos eixos coordenados.

a)   Escreve uma equação vectorial da recta que contém [AB].

a)   Escreve a equação reduzida da recta que contém [AB].

b)   Mostra que qualquer rectângulo definido por P e pelos semieixos positivos, como mostra a figura, tem perímetro 16.

Nota:  Para perceber a relação obtida, utiliza o seguinte sketch GSP:
http://www.prof2000.pt/users/amma/recursos_materiais/rec/10_ano/f_trab/2002_03/ft_16_1.gsp

Solução

8.   Para cada , a expressão  define uma função afim.

a)   Se , determina analiticamente as coordenadas dos pontos de intersecção do gráfico da função com os eixos coordenados.

b)   Determina a de modo que o gráfico da função contenha o ponto de coordenadas (1, 3).

c)   Indica o valor de a de modo que f não tenha zeros.

d)   Determina a de modo que a função seja decrescente.

Solução

9.   Um rato está a ser perseguido por um gato.
Às 20 h 52 min 3 s o rato leva 5 metros de avanço sobre o gato.
As velocidades de corrida do gato e do rato são consideradas constantes e são, respectivamente, 8 m/s e 6 m/s.

Nota:  Começa por explorar os recursos disponíveis (folha de cálculo e programa Modellus) na actividade “Um gato e um rato”, em:
http://www.prof2000.pt/users/amma/recursos_materiais/alabmat/viseumat6_10.htm

a)   O que representam as expressões    e  ?

b)   Determina a hora em que o gato alcançou o rato.
Resolve o problema analítica e graficamente.

Solução

 

 

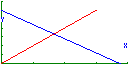
Nos exercícios 10 e 11, além da resolução analítica, apresenta também uma exploração gráfica das situações

10. As cidades do Porto e Lisboa estão a 300 Km de distância e são servidas por uma linha de caminho de ferro. À mesma hora partem dois comboios directos (não param em nenhuma estação), um de Lisboa com destino ao Porto e outro do Porto com destino a Lisboa. O comboio que se dirige para Lisboa tem uma velocidade constante de 100 Km/h. O que se dirige para o Porto tem uma velocidade constante de 80 Km/h.

Quanto tempo depois de partirem é que os comboios se encontram?

Solução

11. O Fernando e a irmã vivem à beira de uma estrada que conduz a um castelo situado a 5 Km de distância. Ambos trabalham no Castelo, ela no período da manhã e ele no período da tarde. Cruzam-se sempre no caminho para que ela lhe possa entregar a chave do Castelo. Ele sai de casa às 12 horas e demora 15 minutos a fazer cada quilómetro. À mesma hora a sua irmã sai do Castelo e dirige-se para casa demorando 20 minutos para percorrer cada quilómetro.

A que horas se cruzam?
Quando se cruzam, a que distância está o Fernando do Castelo?
Qual te parece ser o horário de visita do Castelo?

 Solução

 

 

 

 

SOLUÇÕES

1.  

2.  

3.  
        

4.  

a)   .

b)   .
   

5.  

a)   .

b)   0 e 12, .2 e 10, 3 e 9 (p.e.).

c)   Designando por y o maior dos números, vem:

Os dois números são: 4 e 8.
   

6.  

a)   Para que o triângulo [AOC] tenha 1,5 de área, o ponto A tem de possuir as coordenadas (1, 0).
Assim,  é a equação reduzida da recta AC, pois  e C (0, 3).

b)   Para que o triângulo [BOC] seja isósceles, o ponto B tem de possuir as coordenadas (3, 0).
Assim,  é a equação reduzida da recta BC, pois  e C (0, 3).

7.  

a)   Como  é colinear com , então  é uma equação vectorial da recta considerada.

b)   Logo,  é a equação reduzida dessa recta, pois  e .

c)   Sugestão: Utiliza o sketch sugerido.

8.  

a)   Para  vem . Donde, fazendo  vem  e fazendo  vem .
Portanto, (0,  ) e ( , 0) são as coordenadas dos pontos pedidos.
        

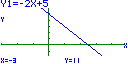
b)   Para que o gráfico da função contenha o ponto considerado, as suas coordenadas (1, 3) terão de verificar a expressão dada. Logo, .
   

c)   Para que a função afim  não tenha zeros, terá de ser .
Como , então terá de ser .

d)   A função afim  é estritamente crescente para  e estritamente decrescente para .
Logo, terá de ser .

9.  

a)   Representam as distâncias, respectivamente, do rato e do gato, ao fim de t segundos após as 20 h 52 min 3 s, relativamente ao ponto em que o gato se encontrava nesse momento.

b)   O gato alcança o rato no instante em que essas distâncias se igualarem. Logo, .
Portanto, o gato alcança o rato às 20 h 52 m 5, 5 s, ou seja, 2,5 segundos após esse instante (20 metros depois).
   

Recorrendo às tabelas de valores geradas por essas funções poder-se-ia também tentar descobrir esse instante:
            

10. Os comboios encontram-se passado 1 hora e 40 minutos (5/3 da hora).
   

y  distância ao Porto (Km); x  tempo (h)

11. Cruzam-se, aproximadamente, às 12 h 42 m 51 s. (  horas)
Quando se cruzam, o Fernando está aproximadamente a 2,143 Km do Castelo. (  Km)
   

y  distância a casa (Km); x  tempo (h)