Escola
Secundária/3 da Sé-Lamego
Ficha de
Trabalho de Matemática
Ano Lectivo 2002/03 Circunferência,
círculo, elipse, superfície esférica e esfera 10.º Ano
1.
A
equação define uma circunferência.
a)
Indica o centro e o raio dessa circunferência.
b)
Desenvolve os casos notáveis e representa a equação na
forma .
Solução
2. Averigua se as equações seguintes representam ou não
circunferências e, em caso afirmativo, indica os respectivos centro e raio.
a)
b) c)
Solução
3. Caracteriza
por uma condição cada uma das seguintes regiões planas coloridas:
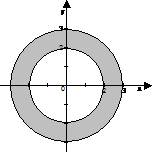

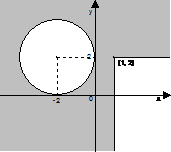
Solução
4.
Determina a equação reduzida da elipse definida por .
Solução
5. Determina a equação reduzida da elipse de focos F (3, 0) e
F’ (-3, 0) e semieixo maior igual a 5.
Solução
6. A elipse de equação está inscrita num rectângulo de lados 2a (horizontal) e 2b (vertical).
Justifica que a circunferência de centro B e raio a corta o eixo Ox em F e F’ (focos da elipse).
Solução
7. Partindo da circunferência de equação ,
encontra uma equação da figura geométrica que dela se obtém quando cada ponto M
(x, y) é transformado noutro, M’ (x’, y’) em que e .
Solução
8. A condição representa uma esfera.
Determina o centro e o raio.
Solução
9.
a)
Determina uma condição que defina a parte da esfera
representada, sabendo que o raio do círculo de centro C’ (distância de C’ a A)
é e que esse círculo é paralelo ao plano
xOy.
b)
O sólido da figura intersecta algum dos planos
coordenados? Justifica.
Solução
10. Determina o centro e o raio da circunferência
definida pela condição:
.
Solução
11. Qual o lugar geométrico dos pontos do espaço que
obedecem à condição (em )?
Solução
12. Observa a figura ao lado.
Ox e Oy são eixos de simetria do rectângulo [ABCD]
inscrito na circunferência.
O ponto A tem as coordenadas (-2, 3).
Determina:
a)
As coordenadas dos pontos B, C e D.
b)
A distância de A a C.
c)
A medida da área tracejada.
Solução
13.
[EFGH] é um
rectângulo inscrito na circunferência de centro (0, 0) e raio 5 unidades.
a)
Escreve a equação da circunferência.
b)
Qual é a ordenada de F sabendo que a sua abcissa é 4?
c)
Determina uma condição que caracterize a região sombreada
da figura.
Solução
14.
O círculo da figura ao lado, de centro (0, 0) e raio 3, está
dividido em três regiões pintadas de cores diferentes.
a)
Qual será a região de maior área? E de maior perímetro?
Confirma a tua conjectura efectuando os cálculos necessários
b)
Determina uma condição que defina a região 1.
Solução
15.
Escreve a equação da superfície esférica de centro no ponto de
coordenadas (-1, 2, 0) e tangente ao plano de equação .
Solução
16.
Identifica a superfície esférica definida pela equação .
Solução
17.
Qual o valor real que deve ter o parâmetro m para que a equação represente:
a)
um ponto? (indica as coordenadas desse ponto)
b)
um conjunto vazio?
Solução
18.
Relaciona m e a (parâmetros reais) de forma que a
equação represente uma superfície esférica de raio 4.
Solução
19.
Determina o centro e o raio da circunferência definida por: .
Solução
20.
Determina a equação reduzida da elipse formada pelos pontos cuja
soma das distâncias a e é 12 unidades.
Solução
21.
Determina a equação reduzida da elipse cujo semieixo maior é 5,
tem centro em (0, 0) e passa pelo ponto (4, 1).
Solução
22.
Caracteriza por uma condição a seguinte região sombreada:
Solução
23.
Considera a circunferência de centro no ponto de coordenadas (1,
-2) e raio .
Indica as coordenadas de três pontos de modo que um seja interior, outro
exterior e o terceiro pertencente à circunferência.
Solução
24.
Descreve o conjunto de pontos do espaço representados por cada
uma das seguintes condições:
a)
b) c)
Solução
25.
Na figura estão representadas duas circunferências concêntricas
de centro C (2, 3). Uma contém o ponto (2, 0) e a outra o ponto de coordenadas
(0, 3).
As rectas r e s são paralelas aos eixos coordenados.
A recta s contém o ponto de coordenadas (0, 4) e a recta r contém o ponto de
coordenadas (1, 0).
Define por uma condição o conjunto de pontos de coordenadas representado a sombreado
na figura.
Solução
26.
Como sabes, a Terra move‑se à volta do Sol com uma órbita elítica
e o Sol ocupa um dos seus focos. Em termos aproximados, o semieixo maior da
órbita tem 149 milhões de quilómetros de comprimento e a excentricidade é .
Desprezando os seus raios, determina, em Km:
a)
a distância mais curta entre a Terra e o Sol;
b)
a maior distância entre o Sol e a Terra.
NOTA: A excentricidade
e de uma elipse com semieixo maior a ou b e semi‑distância focal c
é ou ,
respectivamente.
Solução
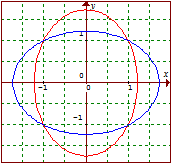
27.
Considera as duas elipses de equações e .
Indica as coordenadas dos pontos de intersecção com os eixos e representa as
duas elipses no mesmo referencial.
Obtém as coordenadas dos pontos de intersecção das duas elipses.
NOTA: Tenta resolver o problema recorrendo à
visualização e às simetrias das elipses.
Solução
28.
Considera, num referencial do espaço, uma esfera de centro na
origem e raio r. Define o conjunto dos pontos da superfície esférica que estão
à distância k do plano xOy.
Discute a influência da relação entre k e r neste conjunto de pontos.
Solução
SOLUÇÕES
1.
a)
C (-1, 3) e
b)
2.
a)
C
(2, -3) e
b)
C (-1,
-2) e
c)
Conjunto
vazio
3.
a)
b)
c)
4.
5.
6.
7.
(elipse)
8.
C (3, -1, 1) e
9.
a)
b)
Apenas intersecta o plano yOz.
10. C (1, 0, 1) e
11. Superfície cilíndrica que
intersecta o plano xOy segundo uma circunferência de centro (3, -5, 0) e raio 2
unidades.
12.
a)
B
(2, 3); C (2, -3) e D (-2, -3)
b)
c)
(2 c.d.)
13.
a)
b)
-3
c)
14.
a)
e
b)
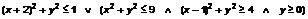
15.
16. Superfície esférica de
centro (2, -4, 1) e raio 3
17.
a)
;
C (2, -4, 1)
b)
18.
19. C (-1, 1, 0) e
20.
21. Para : ;
Para :
22.
23. Interior: A (1, -2) (p.e.);
Exterior: B (1, 1) (p.e.);
Na circunferência: C (1, -2+ ) (p.e.)
24.
a)
Esfera de centro na origem e raio 4.
b)
Conjunto de pontos do espaço que não pertencem à esfera de
centro no ponto de coordenadas (1, -2, 3) e raio .
c)
Círculo em ,
pertencente ao plano xOy, centrado em (0, 0, 0) e de raio 2.
25.
26.
a)
146.467.000
Km
b)
151.533.000
Km
27. ( ,
0); ( ,
0); (0, );
(0, ).
( ,
0); ( ,
0); (0, );
(0, ).
(1, 1); (-1, -1); (1, -1) e (-1, 1).
28. O lugar geométrico dos
pontos que estão a uma distância dada de um plano são dois planos paralelos a
ele.
Neste caso, os planos de equações e .
Se ,
os planos não intersectam a superfície esférica e o conjunto de pontos é vazio.
Se ,
o corte são dois pontos:
(0,
0, k) e (0, 0, -k).
Se ,
os cortes são duas circunferências:
.
O Professor