Escola Secundária da Sé-Lamego

Ficha de Trabalho de Matemática

NÚMEROS IRRACIONAIS

Números irracionais são números que não é possível representar na forma de fracção, isto é, que não podem ser escritos como razão de dois números inteiros.

As dízimas dos números irracionais são sempre infinitas não periódicas.

O conjunto dos números reais, R, compreende os números racionais e irracionais.

As dízimas finitas e as dízimas infinitas periódicas representam sempre números racionais.

Por exemplo, determinemos a fracção correspondente ao número racional :

Designando  por , temos:

              subtraindo ordenadamente, vem:

Logo, .

Um irracional famoso

Talvez o mais famoso número irracional seja o PI (  ), o quociente entre o perímetro e o diâmetro de um círculo. As calculadoras científicas têm uma tecla para acesso directo a um valor aproximado de  com dez, ou mais, dígitos. Por vezes, quando se calcula o perímetro ou uma área de um círculo utiliza‑se  como valor aproximado de , mas actualmente ele já foi calculado com milhões de casas decimais.

OPERAÇÕES COM RADICAIS

Em certas situações particulares é possível operar com raízes quadradas, raízes cúbicas, ....

Radicais equivalentes

A propriedade seguinte tem duas aplicações: simplificação de radicais e redução de radicais ao mesmo índice.

Exemplos

Adição e subtracção de radicais

É possível traduzir a soma e a diferença de radicais por um único radical quando tiverem o mesmo índice e o mesmo radicando.

Exemplos

Multiplicação de radicais

O produto de dois radicais com o mesmo índice, é um radical ainda com o mesmo índice, cujo radicando é o produto dos radicandos.

Exemplos

Divisão de radicais

O quociente de dois radicais com o mesmo índice, é um radical ainda com o mesmo índice, cujo radicando é o quociente dos radicandos.

Exemplos

Passar um factor para dentro ou para fora do radical

Pode sempre escrever‑se o produto de um número racional por um radical sob a forma de um radical, bastando para isso escrever o número racional na forma de radical e, em seguida, multiplicar os dois radicais.

Exemplos

Potência de um radical

A potência de um radical é um radical ainda com o mesmo índice, cujo radicando é a potência do radicando.

Exemplos

Radical de um radical

O radical de um radical é outro radical cujo índice é o produto dos índices e o radicando é o mesmo número.

Exemplos

RACIONALIZAÇÃO DE DENOMINADORES

Qual dos números,  e , é maior?

Determinar mentalmente um valor aproximado de  é relativamente fácil, pois sabemos que  é um valor aproximado de  às décimas. Mas, determinar mentalmente um valor aproximado de  já não é tarefa fácil.

Bem... quem diria que as fracções são equivalentes?!  Com efeito,            .

O denominador da fracção  é um número irracional, enquanto o denominador de  é um número racional. Diz‑se que racionalizámos o denominador da primeira fracção. Esta é a transformação que, por norma, se aplica a todos os resultados em forma de fracção com denominador irracional.

Exemplos

ENQUADRAMENTOS

Há muitas situações em que se torna útil, e mesmo necessário, conhecer enquadramentos para os resultados de adições e multiplicações em que intervêm valores aproximados.

Enquadramento da soma

Calculemos um valor aproximado de .

Sabendo que  e que , utilizemos, por exemplo, valores aproximados a menos de uma centésima:

             adicionando ordenadamente, vem:

 é um valor aproximado da soma , por defeito;

 é um valor aproximado da soma , por excesso;

Qualquer número compreendido entre  e  é um valor aproximado de  com erro inferior a  (  ), ou seja, um valor aproximado da soma a menos de duas centésimas.

Diz‑se que  é um majorante do erro cometido naquela aproximação.

Enquadramento do produto

Calculemos um valor aproximado de .

Sabendo que  e que , utilizemos, por exemplo, valores aproximados a menos de uma décima:

                  multiplicando ordenadamente, vem:

 é um valor aproximado do produto , por defeito;

 é um valor aproximado da soma , por excesso;

Qualquer número compreendido entre  e  é um valor aproximado de  com erro inferior a  (  ), ou seja, um valor aproximado da soma a menos de 54 centésimas.

Diz‑se que  é um majorante do erro cometido naquela aproximação.

EXERCÍCIOS

1.    Calcule:

a)           b)                             c)           d) 

2.    Calcule

a)                        b)                       c)  

3.    Calcule:

a)                                    b)                                 c)  

4.    Calcule:

a)                                     b)                                           c)  

5.    Calcule:

a)                                   b)                                    c)  

6.    Simplifique cada uma das expressões:

a)                                           b)                         c)  

7.    Efectue as operações indicadas e apresente o resultado na forma mais simples:

a)                         b)               c)                              d)               e)  

b)                g)                     h)              i)          j)   

8.    Racionalize os denominadores das seguintes expressões:

a)                                       b)                                      c)                                 d) 

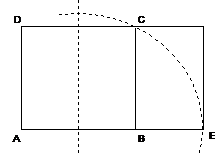
9.    Considere um quadrado [ABCD] com  dm de lado.
Determine a mediatriz de [AB].
Com centro no ponto médio de [AB] trace um arco de circunferência que passe por C até encontrar o prolongamento de [AB] para o lado de B no ponto E.
Desenhe o rectângulo de lados [AD] e [AE].

a)    Determine o comprimento exacto do lado maior do rectângulo (  ).

b)   Sabendo que , entre que valores varia o lado maior do rectângulo?

c)    Determine o perímetro exacto do rectângulo.

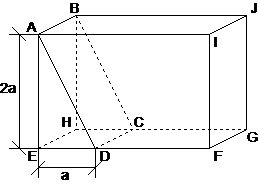
10. A figura representa um paralelepípedo rectângulo seccionado pelo plano ABC que o separou em dois sólidos diferentes.

 cm

O volume do sólido menor resultante da divisão é  cm³.

a)    Determine .

b)   Determine o volume do sólido maior obtido no corte.

11. Considere um prisma quadrangular regular em que a altura é o dobro da aresta da base.

a)    Representando por a a aresta da base, obtenha as medidas de todas as diagonais do prisma.

b)   Determine a medida da aresta da base para que o volume seja  cm³.

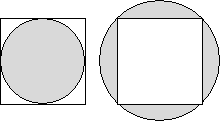
12. Desenhe um quadrado e um círculo inscrito.
Calcule o perímetro e a área do círculo inscrito num quadrado de lado 1.
Indique o valor exacto e um valor aproximado.

13. Desenhe um quadrado e um círculo circunscrito.
Calcule o perímetro e a área do círculo circunscrito a um quadrado de lado 1.
Indique o valor exacto e um valor aproximado.

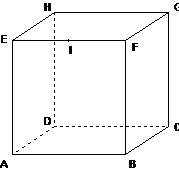
14. Considere o cubo da figura.
I é o ponto médio de [EF.

a)    Desenhe a secção resultante da intersecção do cubo pelo plano CIH. Explique o seu raciocínio.

b)   Classifique, justificando, o quadrilátero obtido.

c)    Calcule o valor exacto do perímetro da secção, sabendo que o comprimento da aresta é  cm.

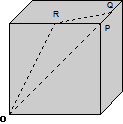
15. Duas formigas vão de O a Q pelas paredes de um cubo, à mesma velocidade (R e Q são os pontos médios das arestas). A formiga A segue o trajecto ORQ e a formiga B o OPQ.

a)    Qual das formigas chega primeiro?

b)   Sabendo que a aresta do cubo é  dm, determine a diferença dos comprimentos dos trajectos, com aproximação à décima de milímetro.

SOLUÇÕES

1.    ;   ;   ;   .

2.    3;   ;   .

3.    ;   1;   .

4.    2;   ;   .

5.    ;   ;   .

6.    ;   ,   .

7.    ;   ;   ;   5;   ;   ;   ;   ;   ;   .

8.    ;   ;   ;   .

9.     dm;   Varia entre 1,618 dm e 1,619 dm;   (  ) dm.

10.  cm;   245 cm³.

11. ;   ;   ;    cm.

12. ;   3,14.   ;   0,79.

13. ;   4,44.   ;   1,57.

14. (  ) cm.

15. Trajecto ORQ: ; Trajecto OPQ:  (designando a a medida da aresta).  17,8 milímetros.

O Professor