A Casinha da Matemática

A Álgebra é generosa; ela frequentemente dá mais do que aquilo que lhe é pedido. (D'Alembert)

Tagged: Módulo inicial

0

10.º Ano / Aplicando / Módulo inicial

Uma caixa com latas de refrigerante

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 31

Enunciado

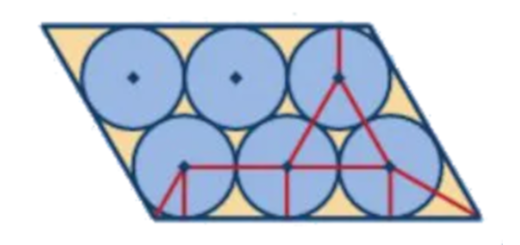
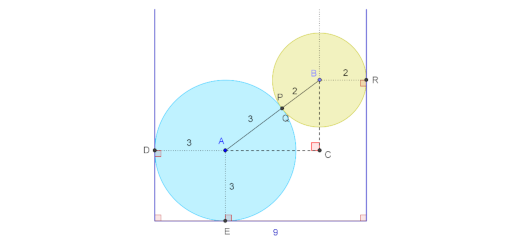
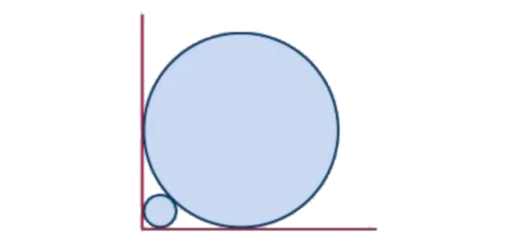
Imagine que alguém pensou acondicionar latas de $75$ cl de refrigerante numa caixa prismática cuja base é um paralelogramo obliquângulo, como mostra a figura.

  1. Se o raio da base de cada lata medir $4$ cm, qual é a área da base da caixa?
    Sugestão: No esquema, marcaram-se vários raios de circunferências. Recorrendo aos seus conhecimentos sobre triângulos (acutângulos ou retângulos) ou ao Teorema de Pitágoras, determine o comprimento e a altura do paralelogramo.
  2. As latas têm
… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

Dois quadrados sobrepostos

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 30

Enunciado

Dois quadrados congruentes de $6$ cm de lado estão sobrepostos como mostra a figura.

O vértice de um dos quadrados está no centro do outro quadrado.

Qual é a área da parte sobreposta?

Resolução >> Resolução

<< Enunciado… Ler mais
2

10.º Ano / Aplicando / Módulo inicial

A pirâmide de Quéops

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 39 Ex. 30

Enunciado

Conta-se que Thales de Mileto (séc. VI a.C.), considerado por alguns autores como um dos sete sábios da Antiguidade, se ofereceu para determinar a altura da pirâmide de Quéops, sem escalar o monumento.

Segundo a lenda, a prova ter-se-á realizado na presença do faraó Amasis. Thales espetou perpendicularmente ao chão a sua bengala e mediu as sombras da bengala e da pirâmide. Após os cálculos rápidos, Thales obteve a resposta desejada.

Em que se baseou o … Ler mais

0

10.º Ano / Aplicando / Módulo inicial

Em volta de um retângulo

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 29

Enunciado

Observe a figura ao lado, onde [ABCD] é um retângulo.

  1. Se o segmento de reta [AM] é perpendicular a BD, demonstre que os triângulos [MAD] e [ABD] são semelhantes.
  2. Se AM e PC são paralelas e AM e BD são perpendiculares, demostre que os triângulos [MAD] e [PBC] são semelhantes e conclua que $\frac{{\overline {AD} }}{{\overline {PC} }} = \frac{{\overline {MD} }}{{\overline {BP} }}$.
  3. Se PC é perpendicular a BD, demonstre que $\frac{{\overline {NC} }}{{\overline {NB} }}
… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

Duas circunferências concêntricas

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 27

Enunciado

Os raios de duas circunferências concêntricas medem $4$ cm e $5$ cm.

Determine o comprimento da corda da circunferência maior que é tangente à circunferência menor.

Resolução >> Resolução

<< Enunciado… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

Resolva as equações

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 38 Ex. 26

Enunciado

Resolva, em $\mathbb{R}$, as seguintes equações:

  1. $$\frac{{2\left( {x + 1} \right)}}{3} + 5\left( {x + 2} \right) = 8 – 3x$$
  2. $$3\left( {\frac{{x + 1}}{2} + \frac{{x – 1}}{3}} \right) = 5x – 2$$
  3. $$5 – \frac{{2\left( {x + 1} \right)}}{4} = \frac{{3x – 1}}{7}$$
  4. $$\frac{{x + 4}}{6} – \frac{{2\left( {x + 1} \right)}}{9} = \frac{{x – 2}}{6} + \frac{{11 – 2x}}{{18}}$$
  5. $$\left( {3x – \frac{2}{3}} \right)\left( {3x + \frac{2}{3}} \right) – 4 = {\left( {3x –
… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

Duas esferas e um cilindro

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 37 Ex. 19

Enunciado

Duas esferas, de raios $2$ e $3$, estão encaixadas num recipiente cilíndrico de diâmetro $9$ (unidades em centímetro).

  1. Faça um desenho e explique a sua construção.  
  2. Qual é o volume de líquido necessário para cobrir totalmente as duas esferas.  
  3. Se o líquido cobrir exatamente a esfera maior, que se encontra no fundo, que parte da esfera menor fica fora?

Resolução >> Resolução

<< Enunciado… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

O caracol e a alface

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 36 Ex. 16

Enunciado

Um caracol colocado em $C$ quer atingir uma alface em $A$.

Para isso, tem de escalar uma placa de vidro [de espessura desprezável], com $0,75$ m de altura.

A distância do caracol à placa é $1,5$ m e da placa à alface é de $1$ m.

Na figura está representado, a vermelho, um exemplo de trajeto que o caracol pode seguir.

Se a sua velocidade é de $5$ km/h, quanto tempo, no mínimo, terá de esperar até … Ler mais

0

10.º Ano / Aplicando / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 4

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 14

Enunciado

Desenhe um quadrilátero qualquer e o paralelogramo que se obtém unindo consecutivamente os pontos médios dos lados desse quadrilátero.

  1. Suponha que as diagonais do quadrilátero dado medem $10$ cm e $6$ cm.
    Quanto medem os lados do novo quadrilátero?
  2. Confirme que o perímetro do paralelogramo é igual à soma das diagonais do quadrilátero original.
  3. Investigue qual é a relação entre as áreas do quadrilátero dado e a do paralelogramo.

Resolução >> Resolução

<< Enunciado… Ler mais
0

10.º Ano / Aplicando / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 3

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 13

Enunciado

Unindo os pontos médios dos lados consecutivos de um quadrilátero, podemos obter um trapézio não paralelogramo? E um losango? Em que condições?

Resolução >> Resolução

<< Enunciado… Ler mais
1

10.º Ano / Aplicando / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 2

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 35 Ex. 12

Enunciado

A que condição deve obedecer um quadrilátero convexo para que, unindo os pontos médios dos lados consecutivos, se obtenha:

  1. um retângulo;
  2. um quadrado.

Resolução >> Resolução

<< Enunciado… Ler mais
3

10.º Ano / Aplicando / Módulo inicial

Unindo os pontos médios dos lados de um quadrilátero – Parte 1

Módulo inicial: Matemática A 10.º - Parte 1 - Pág. 24 TAREFA

Enunciado

Determine três, ou mais, quadriláteros como os que se seguem.

  1. Determine os pontos médios dos lados dos quadriláteros e, em cada um deles, construa os segmentos de reta definidos por pontos médios de lados consecutivos.
  2. Investigue que tipo de quadriláteros obteve. Registe as suas conjeturas e tente justificá-las.
  3. Recorrendo a propriedades estudadas, prove, por exemplo, que o polígono que se obtém unindo os pontos médios dos lados consecutivos do quadrilátero [ABCD] é um paralelogramo.

R1 … Ler mais