A Casinha da Matemática Blog
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 110 Tarefa 8
Enunciado
Considera a função definida, no conjunto dos números reais, por \(f\left( x \right) = 3{x^2}\).
- Esboça o gráfico de f num referencial cartesiano.
- Determina graficamente as soluções da equação \(3{x^2} = 12x\), determinando a interseção dos gráficos da função quadrática f e da função afim g, definida por \(g\left( x \right) = 12x\).
- Determina analiticamente as soluções da equação \(3{x^2} = 12x\).
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 110 Tarefa 7
Enunciado
Considera uma função f quadrática representada graficamente no referencial cartesiano da figura por uma parábola de eixo vertical e que passa na origem.
Sabendo que o ponto de coordenadas \(\left( { – 2,\; – 1} \right)\) pertence ao gráfico de f, determina a expressão algébrica de f.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 108 Tarefa 6
Enunciado
A Clara criou um logótipo, usando quatro quadrados geometricamente iguais, conforme indica a figura.
Três partes estão pintadas a vermelho e uma está pintada a azul.
Considera x o comprimento, em centímetros, do lado do quadrado azul.
- Seja y a área do quadrado azul em função de x.
- Copia e completa a tabela.
- Representa, num gráfico, os pontos registados na tabela anterior.
- Escreve uma expressão algébrica que relacione x
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 107 Ex. 8
Enunciado
Na figura, estão representados, num referencial cartesiano, os pontos A e B e partes dos gráficos de duas funções, f e g.
Sabe-se que:
- o ponto O é a origem do referencial;
- a função f é uma função de proporcionalidade direta;
- a função g é uma função de proporcionalidade inversa;
- o ponto A pertence ao gráfico de f e tem coordenadas \(\left( {8,\;6} \right)\);
- o ponto B pertence ao gráfico de f e ao gráfico de
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 107 Ex. 7
Enunciado
No referencial cartesiano da figura, está representada parte do gráfico da função f definida por \(y = \frac{{10}}{x}\), com \(x > 0\).
Sabe-se que:
- os pontos P e Q pertencem ao gráfico da função f;
- os pontos A e B pertencem ao eixo das abcissas;
- o ponto C pertence ao eixo das ordenadas;
- as abcissas dos pontos A e P são iguais,
- as abcissas dos pontos B e Q são iguais.
- Qual é a área do
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 107 Ex. 6
Enunciado
Observa o gráfico da função f.
- Verifica que a função f é de proporcionalidade inversa e determina a constante de proporcionalidade.
- Escreve uma expressão algébrica da função representada no gráfico.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 106 Ex. 5
Enunciado
A Ana e o Bernardo estavam a dividir uma tablete de chocolate. Como a tablete tem 12 quadrados, cada um deles iria comer 6. Entretanto, chegaram a Marta e o Gonçalo que também quiseram chocolate, logo, coube a cada um 3 quadrados.
- Copia e completa a seguinte tabela, em que n é o número de amigos e q é o número de quadrados de chocolate que cada um irá comer.
…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 106 Ex. 4
Enunciado
Considera a função f de proporcionalidade inversa representada graficamente no referencial cartesiano da figura.
- Tendo em conta os dados da figura, determina o valor de b.
- Se \(a = 4\), indica a constante de proporcionalidade inversa e uma expressão algébrica da função f.
Resolução >>
Resolução
<< Enunciado…
Ler mais
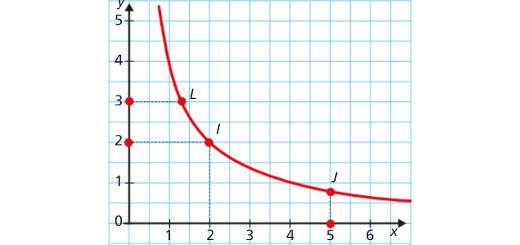
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 106 Ex. 3
Enunciado
Considera a função de proporcionalidade inversa representada graficamente no referencial cartesiano da figura.
- Determina a expressão algébrica da função f, identificando a constante de proporcionalidade inversa.
- Determina a abcissa do ponto L e a ordenada do ponto J.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 106 Ex. 2
Enunciado
Sejam X e Y duas grandezas inversamente proporcionais.
Sabe-se que quando a medida de X é 3, a medida de Y é 4.
Determina uma expressão algébrica para a função de proporcionalidade inversa associada.
Resolução >>
Resolução
<< Enunciado…
Ler mais
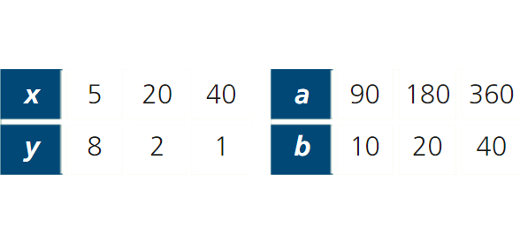
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 106 Ex. 1
Enunciado
Observa as tabelas.
- Há algum tipo de proporcionalidade entre as grandezas x e y?
E entre as grandezas a e b?
- Determina, quando existir, a constante de proporcionalidade.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 102 Ex. 6
Enunciado
Um comboio que anda à velocidade média de 75 km/h faz um certo percurso em 36 minutos.
Quanto tempo demoraria a fazer o mesmo percurso se andasse a uma velocidade média de 45 km/h?
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 102 Ex. 5
Enunciado
Para se embalar a produção diária de ovos da empresa Aves são necessárias 120 caixas. Em cada caixa colocam-se duas dúzias e meia de ovos.
Quantas caixas são necessárias para embalar a mesma produção diária, se se usarem caixas de duas dúzias de ovos?
Mostra como chegaste à tua resposta.
Resolução >>
Resolução
<< Enunciado…
Ler mais
Proporcionalidade inversa e Funções algébricas: Matematicamente Falando 9 - Parte 2 Pág. 102 Ex. 2
Enunciado
Sabendo que a e b são grandezas inversamente proporcionais, copia e completa a seguinte tabela.
Resolução >>
Resolução
<< Enunciado…
Ler mais